Matura z matematyki - ~Suma częściowa ciągu

Sumy częściowe

Suma częściowa ciągu to inaczej suma kilku kolejnych wyrazów pewnego ciągu. Najprostszym przykładem może być $a 1 + a 2$ , czy też $a 2 + a 4 + a 6$ dla pewnego ciągu $(a n)$ .

Policzmy sumę czterech kolejnych wyrazów ciągu $(a n)$ zdefiniowanego wzorem $a_n = 2 cdot |n-3|$ . Mamy $a_1 = 2 cdot |1-3| = 2 cdot 2 = 4$ , $a_2 = 2 cdot |2-3| = 2$ , $a_3 = 2 cdot |3-3| = 0$ , $a_4 = 2 cdot |4-3| = 2$ , czyli:

a 1 + a 2 + a 3 + a 4 = 4 + 2 + 0 + 2 = 8

Podobnie policzmy sumę wyrazów $c 2 + c 10 + c 30 + c 51 + c 1001$ ciągu arytmetycznego $(c n)$ , gdzie $c 1 = 10$ , a różnica ciągu wynosi -3. Jednak najpierw musimy policzyć ile wynoszą odpowiednie wyrazy. Ze wzoru na n-ty wyraz ciągu arytmetycznego mamy:

$c_2 = 10 + (2-1)cdot(-3) = 7$

$c_{10} = 10 + (10-1)cdot(-3) = -17$

$c_{30} = 10 + 29 cdot (-3) = -77$

$c_{51} = 10 + 50 cdot (-3) = -140$

$c_{1001} = 10 + 1000 cdot (-3) = -2990$

Zatem suma $c 2 + c 10 + c 30 + c 51 + c 1001 = 7 - 17 - 77 - 140 - 2990 = - 3217$ .

Sumę kolejnych n kolejnych wyrazów pewnego ciągu, czyli $a_1 + a_2 + a_3 + a_4 + dots + a_n$ z reguły oznaczamy jako $S n$ . Kilka przykładów ...:

S 5 = a 1 + a 2 + a 3 + a 4 + a 5

S 3 = a 1 + a 2 + a 3

$S_{50} = a_1 + a_2 + a_3 + a_4 + dots + a_{50}$

S 1 = a 1

Używając tego oznaczenia możemy zapisać także sumę kolejnych, ale nie koniecznie początkowych wyrazów, na przykład:

a 3 + a 4 + a 5 = (a 1 + a 2 + a 3 + a 4 + a 5) - (a 1 + a 2) = S 5 - S 2

a 5 + a 6 + a 7 = (a 1 + a 2 + a 3 + a 4 + a 5 + a 6 + a 7) - (a 1 + a 2 + a 3 + a 4) = S 7 - S 4

$a_{50} + a_{51} + a_{52} + dots + a_{100} = (a_1 + a_2 + dots + a_{49} + a_{50} + dots + a_{100}) - (a_1 + a_2 + dots + a_{49}) = S_{100} - S_{49}$

W ogólności suma $a_{k} + a_{k+1} + dots + a_{n} = (a_1 + a_2 + dots + a_{k-1} + a_k + a_n) - (a_1 + a_2 + dots + a_{k-1}) = S_n - S_{k-1}$ .

Suma częściowa ciągu arytmetycznego

TWIERDZENIE

Suma n początkowych wyrazów ciągu arytmetycznego wynosi:

$S_n = a_1 + a_2 + a_3 + dots + a_n = frac{a_1 + a_n}{2} cdot n$

Znając to twierdzenie możemy policzyć sumę $S_{10} = 1 + 2 + 3 + dots + 10$ . Widzimy, że $n = 10$ i ponadto $a 1 = 1$ i $a 10 = 10$ . Zatem $S_{10} = frac{a_1 + a_n}{2} cdot n = frac{1+10}{2} cdot 10 = 55$ .

Korzystając z tego wzoru możemy w bardzo prosty sposób znaleźć wzór na sumę n kolejnych liczb naturalnych. Zero możemy pominąć, ponieważ nic nie wnosi do naszej sumy. Zobaczmy -- pierwszą liczbą będzie 1, czyli $a 1 = 1$ , a n-tą liczbą jest $a n = n$ . Ponadto od 1 do n jest dokładnie n liczb. Czyli mamy wzór:

$S_n = 1 + 2 + 3 + dots + n = frac{1 + n}{2} cdot n = frac{n(n+1)}{2}$ ,

być może już przez niektórych znany.

Policzmy teraz sumę trzydziestu jeden kolejnych wyrazów ciągu $(t n)$ , gdzie $t 1 = 10$ i $r = 4$ . Wiemy, że $n = 31$ , ale nie znamy wartości $t 31$ , dlatego musimy wykorzystać wzór ogólny na n-ty wyraz ciągu arytmetycznego:

$t_{31} = 10 + (31-1) cdot 4 = 10 + 120 = 130$

Teraz tylko zastosować wzór na sumę początkowych wyrazów:

$S_n = t_1 + t_2 + t_3 + dots + t_{31} = frac{t_1 + t_{31}}{2} cdot 31 =$

$= frac{10 + 130}{2} cdot 31 = 2170$ .

Znajdźmy wzór na sume n początkowych wyrazów ciągu znając jedynie n, $a 1$ i r. Wiemy ze wzoru na n-ty wyraz, że $a_n = a_1 + (n-1)cdot r$ . Podstawiając do wzoru na sumę otrzymujemy:

$S_n = frac{a_1 + a_n}{2} cdot n = frac{a_1 + a_1 + (n-1) cdot r}{2} cdot n$

Po drobnym przekształceniach mamy:

$S_n = frac{[2a_1 + (n-1) cdot r] cdot n}{2}$

(suma n początkowych wyrazów ciągu arytmetycznego o różnicy r)

Czy wzór $S_n = frac{a_1 + a_n}{2} cdot n$ jest prawdziwy dla dowolnego ciągu arytmetycznego? Odpowiedź, brzmi tak. Aby się o tym przekonać przedstawimy dowód.

Dowód:

Wiemy, że $S_n = a_1 + a_2 + dots + a_n$ , a ponieważ $(a n)$ jest ciągiem arytmetycznym, więc $a_k = a_1 + (k-1)cdot r$ . Z tych dwóch zależności wynika, że:

$S_n = a_1 + a_2 + dots + a_n = [a_1 + (1-1) cdot r] + [a_1 + (2-1) cdot r] + dots + [a_1 + (n-1) cdot r]$ ,

sumę tę możemy także przepisać jako (idąc od końca do początku):

$S_n = [a_1 + (n-1) cdot r] + [a_1 + (n-2) cdot r] + dots + [a_1 + (2-1) cdot r] + [a_1 + (1-1) cdot r]$

Dodając obydwie sumy do siebie otrzymujemy:

	$S n$	$=$	$[a_1 + (1-1) cdot r]$	$+$	$[a_1 + (2-1) cdot r]$	$+$	$[a_1 + (3-1) cdot r]$	$+$	$dots$	$+$	$[a_1 + (n-1) cdot r]$
$+$	$S n$	$=$	$[a_1 + (n-1) cdot r]$	$+$	$[a_1 + (n-2) cdot r]$	$+$	$[a_1 + (n-3) cdot r]$	$+$	$dots$	$+$	$[a_1 + (n-n) cdot r]$
	$2 S n$	$=$	$[2a_1 + (n-1) cdot r]$	$+$	$[2a_1 + (n-1) cdot r]$	$+$	$[2a_1 + (n-1) cdot r]$	$+$	$dots$	$+$	$[2a_1 + (n-1) cdot r]$

Wszystkie powyższe sumy posiadają n składników, zatem:

$2S_n = [2a_1 + (n-1) cdot r] cdot n$

Po podzieleniu przez dwa mamy:

$S_n = frac{[2a_1 + (n-1) cdot r] cdot n}{2}$

Czyli dochodzimy do wzoru przedstawionego nieco wyżej.

Suma częściowa ciągu geometrycznego

TWIERDZENIE

Suma n początkowych wyrazów ciągu geometrycznego wynosi:

dla ilorazu $q = 1$ :
$S_n = a_1 + a_2 + a_3 + dots + a_n = n cdot a_1$
dla ilorazu $q neq 1$
$S_n = a_1 + a_2 + a_3 + dots + a_n = a_1 cdot frac{1-q^n}{1-q}$

Możemy teraz bez problemu obliczyć sumę stu dwójek, czyli $S_{100} = 2 + 2 + 2 + 2 + dots + 2$ . Nie powinno to sprawić problemu osobie, która nie zna powyższego twierdzenia. Mamy sto dwójek, więc $S_{100} = 100 cdot 2 = 200$ , proste. Oczywiście możemy wykorzystać odpowiedni wzór. Ponieważ $q = 1$ , więc zastosujemy pierwszego wzór otrzymując $S_{100} = n cdot a_1 = 100 cdot 2 = 200$ .

Obliczmy sumę 4 kolejnych wyrazów ciągu $(b n)$ , gdzie:

b 1 = 11

$frac{b_{k+1}}{b_k} = 3 mbox{ dla } k in mathbb{Z}_+$ .

Ponieważ $q = 3$ , więc wykorzystamy wzór dla $q neq 1$ :

$S_4 = a_1 cdot frac{1-q^4}{1-q} = 11 cdot frac{1-3^4}{1-3} = 11 cdot frac{-80}{-2} = 440$ .

Przejdźmy teraz do nieco trudniejszego przykładu. Obliczmy sumę $S_n = 1 + 2 + 4 + 8 + dots + 64$ . Sumę tę tworzą kolejne wyrazy ciągu geometrycznego. Widzimy, że $a 1 = 1$ , ponadto $q = 2$ . Zastanówmy się, z ilu elementów składa się ta suma (czyli ile wynosi n)? Z wzoru ogólnego wynika, że $a_n = 1 cdot 2^{n-1}$ , a z sumy do policzenia, że $a n = 64$ . Więc $a n = 2 n - 1 = 64 = 2 6$ , czyli $n-1=6 implies n=7$ . Ponieważ $q = 2 neq 1$ , więc wykorzystamy wzór drugi:

$S_7 = a_1 cdot frac{1-q^7}{1-q} = 1 cdot frac{1-2^7}{1-2} = frac{-127}{-1} = 127$ .

Obliczmy sumę 9 kolejnych wyrazów ciągu $(s n)$ zdefiniowanego wzorem:

$s_k = 11 cdot (-10)^{k-1} mbox { dla } k in mathbb{Z}_+$ .

Pamiętamy, że każdy ciąg geometryczny zdefiniowany jest wzorem:

$a_k = a_1 cdot q^{k-1} mbox { dla } k in mathbb{Z}_+$

Zauważmy, że gdybyśmy jako $a 1$ podstawili 11, a jako q liczbę -10, otrzymalibyśmy taki sam wzór na n-ty wyraz, jaki ma ciąg $(s n)$ . Zatem musi zachodzić $s 1 = 11$ , a $q = - 10$ . Możemy teraz wyliczyć sumę, a ponieważ 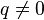$q neq 0$ mamy:

$S_{9} = 11 cdot frac{1-(-10)^{9}}{1-(-10)} = frac{1-(-10)^{9}}{-1} = (-10)^{9} - 1 = -(10^9 + 1)$

Pomyślmy teraz, ile wynosi suma 10 kolejnych wyrazów ciągu zdefiniowanego wzorem:

$c_k = 2 cdot left(-frac{1}{2}right)^{2k}$

Ze wzoru możemy w łatwy sposób wyliczyć kilka pierwszych wyrazów:

$c_1 = 2 cdot left(-frac{1}{2}right)^{2 cdot 0} = 2$

$c_2 = 2 cdot left(-frac{1}{2}right)^{2 cdot 1} = 2 cdot frac{1}{4} = frac{1}{2}$

$c_3 = 2 cdot left(-frac{1}{2}right)^{2 cdot 2} = 2 cdot frac{1}{16} = frac{1}{8}$

...

Zatem widzimy, że $c 1 = 2$ , a $q = frac{c_2}{c_1} = frac{c_3}{c_2} = dots = frac{1}{4}$ . Otrzymujemy:

$S_{10} = 2 cdot frac{1-left(frac{1}{4}right)^{10}}{1-left(-frac{1}{4}right)} = 2 cdot frac{1-left(frac{1}{4}right)^{10}}{frac{5}{4}} = 2 cdot frac{4}{5} cdot (1-left(frac{1}{4}right)^{10}) = frac{8}{5} cdot left[1-left(frac{1}{4}right)^{10}right]$

Wyznaczmy wzór ogólny na sumę n kolejnych elementów ciągu $(d n)$ , w którym $d 1 = 3$ i $q = 5$ . Ponieważ $q neq 1$ możemy ze znanego nam już twierdzenia powiedzieć, że:

$S_n = d_1 cdot frac{1-q^n}{1-q} = 3 cdot frac{1-5^n}{1-5} = 3 cdot frac{(-1) cdot (5^n-1)}{(-1) cdot 4} = 3 cdot frac{5^n-1}{4}$ .

Na koniec spróbujmy udowodnić, że ten wzór jest poprawny, nie odwołując się do wcześniej przedstawionego twierdzenia. Wypiszemy najpierw założenia i tezę, a potem przedstawimy dowód.

Założenia:

$d_k = 3 cdot 5^{k-1}$