Matura z matematyki - ~ Monotoniczność funkcji

DEFINICJA

Funkcja $fcolon X to Y$ jest rosnąca w zbiorze $A subset X$ wtedy i tylko wtedy, gdy dla dowolnych argumentów $x 1$ i $x 2$ należących do zbioru A i $x 1 < x 2$ wynika $f (x 1) < f (x 2)$ .

$x_1 < x_2 implies f(x_1)<f(x_2)$

Inaczej mówiąc wraz ze wzrostem argumentów rosną wartości funkcji.

Analogicznie definiujemy funkcję niemalejącą w zbiorze $A subset X$ , tylko nierówność nie jest ostra. Zachodzi wtedy:

$f(x_1) leq f(x_2)$ , dla

x 1 < x 2

Zauważmy, że gdy nierówność jest rosnąca, to jest również niemalejąca, ale nie musi być odwrotnie.

DEFINICJA

Funkcja $fcolon X to Y$ jest malejąca w zbiorze $A subset X$ wtedy i tylko wtedy, gdy dla dowolnych argumentów $x 1$ i $x 2$ należących do zbioru A i $x 1 < x 2$ wynika $f (x 1) > f (x 2)$ .

$x_1 < x_2 implies f(x_1)>f(x_2)$

Czyli wraz ze wzrostem argumentów maleją wartości funkcji.

Podobnie możemy określić funkcję nierosnącą w zbiorze 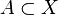$A subset X$ . Mamy wtedy:

$f(x_1) geq f(x_2)$ , dla

x 1 < x 2

Gdy nierówność jest malejąca, to jest również nierosnąca, ale nie musi zajść odwrotnie.

Przykład 1. Przyjrzyjmy się funkcji $y = x 2$ .

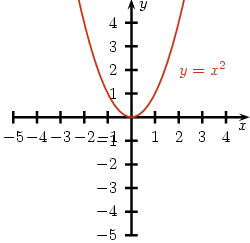
Możemy powiedzieć o tej funkcji, że:

jest rosnąca dla $x > 0$
jest malejąca dla $x < 0$

Przykład 2.

Określmy monotoniczność funkcji na podstawie jej poniższego wykresu. Funkcja ta jest określona dla $x in [-4; 4]$ (czyli $D f = [ - 4;4]$ ).

Z wykresu widzimy, że funkcja ta:

rośnie w przedziałach $( - 4; - 2)$ oraz $( - 1;2)$
maleje w przedziałach $( - 2; - 1)$ oraz $(2;4)$

Przykład 3.

Spójrzmy teraz na najprostszy przykład. Jest to funkcja liniowa $f(x) = frac{4-x}{2}$ . Wykres tej funkcji będzie wyglądał tak:

Widać od razu, że funkcja ta jest malejąca dla wszystkich 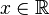$x in mathbb{R}$ .

Przykład 4.

Poniższy wykres przedstawia funkcję niemalejącą.

Nazwa bierze się stąd, że wraz ze wzrostem argumentów nie maleją wartości funkcji, czyli dla coraz wyższych x $f(x) geq f(x_0)$ , gdzie $x 0$ jest dowolną liczbą mniejszą od x.

Przykład 5.

Poniżej przedstawiono wykres funkcji nierosnącej.

Widzimy z wykresu, że wraz ze wzrostem argumentów nie rosną wartości funkcji.

Przykład 6.

Udowodnij na podstawie definicji, że funkcja $f (x) = 2 x + 3$ jest rosnąca.

Funkcję liniową miałeś okazję poznać już w gimnazjum. Wiesz więc od razu, że jeśli współczynnik kierunkowy jest większy od zera to funkcja jest rosnąca. Jednak w zadaniu mam skorzystać z definicji funkcji rosnącej. Czytamy, że funkcja jest rosnąca, gdy dla dowolnego $x 1 < x 2$ zachodzi $f (x 1) < f (x 2)$ .

Weźmy więc dowolne $x 1 < x 2$ i rozwiązmy nierówność $f (x 1) < f (x 2)$ .

$f(x_{1}) = 2 cdot x_{1} + 3 = 2x_{1} + 3$

$f(x_{2}) = 2 cdot x_{2} + 3 = 2x_{2} + 3$

$2 x 1 + 3 < 2 x 2 + 3$

$2 x 1 + 3 - 2 x 2 - 3 < 0$

$2 x 1 - 2 x 2 < 0$

$2 cdot (x_{1} - x_{2}) < 0$

Z założenia mamy, że $x 1 < x 2$ , czyli $x 1 - x 2 < 0$ . A co za tym idzie - wartość w nawiasie jest zawsze ujemna. Iloczyn liczby dodatniej (2) przez dowolną liczbę ujemną jest ujemny. Czyli nierówność $f (x 1) < f (x 2)$ spełniona jest zawsze. Co należało dowieść.