Matura z matematyki - ~ Nierówności kwadratowe

W skrócie

Znalezienie rozwiązania nierówności polega na

obliczeniu miejsc zerowych,
narysowaniu szkicu wykresu funkcji,
wyznaczeniu przedziału, który spełnia nierówność, przy pomocy wykresu.

Dla nierówności dwukwadratowych

rozwiązujemy nierówność ze zmienną pomocniczą (np. $t = x 2$ ),
uzyskane rozwiązania dla t zamieniamy na nierówności i podstawiamy $x 2$ . Rozwiązania otrzymanych nierówności są rozwiązaniem nierówności dwukwadratowej.
np. $t in (4; 5) ; rightarrow ; t>4, , t<5 ; rightarrow ; x^2>4, , x^2<5$ i obliczamy.

Nierówności kwadratowe

Przykład 1. $x 2 - 2 x - 15 > 0$
Przykład 2. $-x^2- 4x + 45 ge 0$
Przykład 3. $x 2 - 5 x + 8 < 0$
Przykład 4. $- x 2 - 6 x - 10 < 0$
Przykład 5. $x 4 + 13 x 2 + 36 > 0$
Przykład 6. $x 2 + 4 x - 12 < 0$

W poprzednim rozdziale dowiedziałeś się, jak rozwiązywać równania kwadratowe. Nierówności kwadratowe rozwiązuję się w nieco odmienny sposób. Poniżej przedstawię podstawowy schemat:

Obliczenie delty i miejsc zerowych
Naszkicowanie prostego wykresu funkcji
Odczytanie z wykresu kiedy nierówność jest spełniona.

Jak zauważyłeś, doszedł nowy element - szkicowanie wykresu. Rozwiążmy sobie przykładową funkcję.

Przykład 1

$x 2 - 2 x - 15 > 0$

Jak przy równościach liczymy deltę i miejsca zerowe:

$Delta = (-2)^2 - 4 cdot 1 cdot (-15) = 64$

$x_{1} = frac{-(-2)-sqrt{64}}{2} = -3$

$x_{2} = frac{-(-2)+sqrt{64}}{2} = 5$

Teraz naszkicujmy prowizoryczny wykres wyrażenia po lewej stronie nierówności. Rysujemy parabole, wiemy o niej, że ramiona są skierowane w górę (a>0) oraz że przecina oś OX w 2 miejscach ( $Δ > 0$ ), wcześniej obliczonych:

Patrzymy na wykres i odczytujemy z niego, kiedy wykres funkcji znajdują się nad osią OX (rozwiązujemy bowiem nierówność f(x)>0), czyli kiedy funkcja przyjmuje wartości dodatnie. Oczywiście wówczas gdy x jest mniejszy od -3 lub większy od 5 (na wykresie -tam, gdzie występuje znak "+"). Zapisujemy to więc:

$x in (-infty, -3) cup (5, +infty)$

W tym miejscu trzeba zwrócić uwagę na parę istotnych szczegółów:

-Nawiasy są "otwarte" ponieważ 0 nie należy do zbioru rozwiązań (f(-3)=0 nie spełnia nierówności f(x)>0),

- $infty$ - nawias po stronie tego oznaczenia jest zawsze otwarty,

-W równaniach rozwiązaniami były pojedyncze liczby. Tutaj rozwiązaniami jest ich cały zbiór.

Przykład 2

$-x^2 - 4x + 45 ge 0$

Podany przykład rozwiążemy podobnie jak poprzedni (według tego samego schematu).

$Delta = (-4)^2 - 4 cdot (-1) cdot (45) = 16 + 180 = 196$

$x_{1} = frac{-(-4) - sqrt{196}}{-2} = frac{4-14}{-2} = 5$

$x_{2} = frac{-(-4) + sqrt{196}}{-2} = frac{4+14}{-2} = -9$

Robimy szkic (a<0 więc ramiona są skierowane w dół):

Widzimy, że wykres jest ponad osią OX w przedziale od -9 do 5. Rozwiązaniem jest więc:

$xin <-9, 5>$

Nawiasy są domknięte, ponieważ 0 należy do zbioru rozwiązań nierówności (f(-9)=0 spełnia nierówność $f(x) ge 0$ .

Przykład 3

$x 2 - 5 x + 8 < 0$

$Delta = (-5)^2 - 4 cdot 1 cdot 8 = 25 - 32 = -7$

$Delta < 0$ - czyli wykres nie ma punktów wspólnych z osią OX. Naszkicujmy wykres:

Parabola w całości znajduję się ponad osią OX. Stąd wniosek, że nierówność nigdy nie jest spełniona. Nie ma rozwiązań, więc:

$x in varnothing$

Przykład 4

$- x 2 - 6 x - 10 < 0$

$Delta = (-6)^2 - 4 cdot (-1) cdot (-10) = 36 - 40 = -4$

$Delta < 0$ - znowu nie ma miejsc wspólnych z osią OX. Szkicujemy pomocniczy wykres (a < 0):

Wykres w całości znajduję się pod osią OX. Oznacza to, że nierówność jest spełniona zawsze.

$x in R$

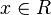
Przykład 5

$x^4 - 13x^2 + 36 ,>, 0$

Przy okazji omawiania równań kwadratowych poznałeś równanie dwukwadratowe. Teraz rozwiążemy nierówność dwukwadratową, w podobny sposób jak równanie.

$t = x^2; ;; t ge 0$

$t^2 - 13t + 36 ,>, 0$

$Delta = (-13)^2 - 4 cdot 1 cdot 36 = 25$

$sqrt{Delta} = 5$

$t_{1} = frac{13 - 5}{2} = 4$

$t_{2} = frac{13 + 5}{2} = 9$

UWAGA!
To, że policzyliśmy wartości $t 1$ i $t 2$ nie oznacza, że już w tym miejscu korzystamy z założenia $t = x 2$ w taki sposób, w jaki używaliśmy go przy równaniach, bowiem jeśli tak to zrobimy, to otrzymane wyniki będą nieprawidłowe! Właśnie tutaj ukazuje się nam różnica pomiędzy równaniami i nierównościami dwukwadratowymi!

Szkicujemy wykres funkcji $t 2 - 13 t + 36 > 0$ i zaznaczamy część dodatnią:

Rozwiązaniem jest:

$t in (-infty, 4) cup (9, +infty)$

Rozwiązaliśmy nierówność ze zmienną pomocniczą t. Potrzeba nam jednak rozwiązać nierówność ze zmienną x. Zapiszmy powyższe rozwiązanie jako koniunkcję dwóch nierówności (zamiast przedziałów):

$t < 4$ lub $t > 9$

Podstawiamy $t = x 2$ i rozwiązujemy dwie nierówności:

$x^2 < 4$ lub $x^2 > 9$

1. $x^2 < 4$

$(x-2)(x+2) < 0$

$x in (-2,2)$ (pomijamy rysowanie wykresu)

2. $x^2 > 9$

$(x-3)(x+3) > 0$

$x in (-infty, -3) cup (3, +infty)$ (także pomijamy rysowanie wykresu)

Rozwiązaniem jest suma rozwiązań 1. i 2.:

$x in (-infty, -3) cup (-2,2) cup (3, +infty)$

Przykład 6

$x 2 + 4 x - 12 < 0$

Ten przykład rozwiążemy nieco innym sposobem niż poprzednie - bez szkicowania wykresu, za pomocą alternatywy układów. Zanim go jednak zaczniesz analizować, przeczytaj informacje o postaci iloczynowej, bowiem właśnie ten element wykorzystamy przy rozwiązaniu tej nierówności.

$Delta = 4^2 - 4 cdot 1 cdot (-12) = 64$

$sqrt{Delta} = 8$

$x_{1} = frac{-4 - 8}{2} = -6$

$x_{2} = frac{-4 + 8}{2} = 2$

Teraz zamieniamy nierówność na postać iloczynową:

$(x - (x 1))(x - x 2) < 0$

$(x + 6)(x - 2) < 0$

Całe wyrażenie jest ujemne gdy:

(x+6) jest dodatnie i (x-2) ujemne lub
(x+6) jest ujemne i (x-2) dodatnie

(iloczyn dowolnej liczby ujemnej, przez liczbę dodatnią jest zawsze ujemny, i na odwrót). Tworzymy w ten sposób alternatywę układów, która wygląda następująco:

$begin{cases} x+6 > 0 x-2 < 0 end{cases}$ lub $begin{cases} x+6 < 0 x-2 > 0 end{cases}$

czyli

$begin{cases} x > -6 x < 2 end{cases}$ lub $begin{cases} x < -6 x > 2 end{cases}$

Rozwiązaniem pierwszego układu jest $x in (-6,2)$ , natomiast drugi układ jest sprzeczny. Rozwiązaniem jest więc:

$x in (-6,2)$