Matura z matematyki - ~Funkcje trygonometryczne kąta ostrego

Funkcje trygonometryczne kąta ostrego

Funkcje trygonometryczne są głównymi pojęciami trygonometrii. Istnieje sześć funkcji trygonometrycznych:

sinus (czyt. sinus), symbol: sin
cosinus (czyt. kosinus), symbol: cos
tangens (czyt. tangens), symbol: tg, tan
cotangens (czyt. kotangens), symbol: ctg, cot, ctn
secans (czyt. sekans), symbol: sec,
cosecans (czyt. kosekans), symbol: cosec, csc

Argumentami funkcji trygonometrycznych mogą być:

kąt skierowany
liczba rzeczywista

DEFINICJA

funkcji trygonometrycznych dla kąta ostrego w trójkącie prostokątnym.

Sinusem kąta ostrego $α$ nazywamy stosunek przyprostokątnej leżącej naprzeciw kąta $α$ do przeciwprostokątnej

$sinalpha = {a over c}$

Cosinusem kąta ostrego $α$ nazywamy stosunek przyprostokątnej leżącej przy kącie $α$ do przeciwprostokątnej

$cosalpha = {b over c}$

Tangensem kąta ostrego $α$ nazywamy stosunek przyprostokątnej leżącej naprzeciw kąta $α$ do przyprostokątnej leżącej przy kącie $α$

$tgalpha = {a over b}$

Cotangensem kąta ostrego $α$ nazywamy stosunek przyprostokątnej leżącej przy kącie $α$ do przyprostokątnej leżącej na przeciw kąta $α$

$ctgalpha = {b over a}$ lub $ctgalpha = {1 over tgalpha}$

Secansem kąta ostrego $α$ nazywamy stosunek przeciwprostokątnej do przyprostokątnej leżącej przy kącie $α$

$secalpha = {c over b}$ lub $secalpha = { 1 over cosalpha}$

Cosecansem kąta ostrego $α$ nazywamy stosunek przeciwprostokątnej do przyprostokątnej leżącej na przeciw kąta $α$

$cscalpha = {c over a}$ lub $cscalpha = {1 over sinalpha}$

Wyznaczanie wartości funkcji trygonometrycznych dla kątów 30°, 45° i 60°

Wyznaczyć wartości funkcji tryg. dla kątów o mierze 30° i 60° można za pomocą trójkąta równobocznego, wykorzystując do tego jego własności.

$sin 30 = frac{frac{a}{2}}{a} = frac{a}{2} cdot frac{1}{a} = frac{1}{2}$
$sin 60 = frac{frac{asqrt{3}}{2}}{a} = frac{asqrt{3}}{2}cdotfrac{1}{a} = frac{sqrt{3}}{2}$
$cos 30 = frac{frac{asqrt{3}}{2}}{a} = frac{asqrt{3}}{2}cdotfrac{1}{a} = frac{sqrt{3}}{2}$
$cos 60 = frac{frac{a}{2}}{a} = frac{a}{2} cdot frac{1}{a} = frac{1}{2}$
$tg 30 = frac{frac{a}{2}}{frac{asqrt{3}}{2}} = frac{a}{2} cdot frac{2}{asqrt{3}} = frac{1}{sqrt{3}} = frac{sqrt{3}}{3}$
$tg 60 = frac{frac{asqrt{3}}{2}}{frac{a}{2}} = frac{asqrt{3}}{2} cdot frac{2}{a} = sqrt{3}$
$ctg 30 = frac{1}{frac{sqrt{3}}{3}} = 1 cdot frac{3}{sqrt{3}} = frac{3sqrt{3}}{3} = sqrt{3}$
$ctg 60 = frac{1}{sqrt{3}} = frac{sqrt{3}}{3}$

A teraz korzystając z własności kwadratu obliczymy wartości funkcji trygonometrycznej dla kąta o mierze 45°.

$sin 45 = frac{a}{asqrt{2}} = frac{1}{sqrt{2}} = frac{sqrt{2}}{2}$
$cos 45 = frac{a}{asqrt{2}} = frac{1}{sqrt{2}} = frac{sqrt{2}}{2}$
$tg 45 = frac{a}{a} = 1$
$ctg 45 = frac{1}{1} = 1$

Z powyższych wyliczeń można stworzyć tabelkę, której będziesz musiał nauczyć się na pamięć.

Wartości funkcji trygonometrycznych dla kąta 30°, 45° i 60°
×	30°	45°	60°
$sin$	$frac{1}{2}$	$frac{sqrt{2}}{2}$	$frac{sqrt{3}}{2}$
$cos$	$frac{sqrt{3}}{2}$	$frac{sqrt{2}}{2}$	$frac{1}{2}$
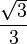$t g$	$frac{sqrt{3}}{3}$	1	$sqrt{3}$
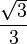$c t g$	$sqrt{3}$	1	$frac{sqrt{3}}{3}$