Matura z matematyki - ~Pojęcie i własności logarytmu

Pojęcie i własności logarytmu

DEFINICJA

Logarytmem liczby dodatniej b przy podstawie a, gdzie $a in mathbb{R}_+ backslash {1}$ , nazywamy wykładnik potęgi c, do której należy podnieść a, aby otrzymać b.

$log_a b=c iff a^c=b$ , dla

a > 0

i $a neq 1$ i

b > 0

a jest podstawą logarytmu

b jest liczbą logarytmowaną

c jest wartością logarytmu

Własności logarytmu:

$a^{log_a b} = b$
$log a 1 = 0$
$log a a = 1$
$log a (m n) = log a m + log a n$
$log_a{m over n} = log_a m - log_a n$
$log a n b = b log a n$
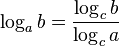
$log_a b = frac{ log_c b}{ log_c a }$
$a > 1 and log_a b > log_a c iff b > c$
$a < 1 and log_a b > log_a c iff b < c$
warto dodać, że logarytm jest funkcją ciągłą

Przykłady

log 10 100 = 2

log 10 10000 = 4

$100 < 1000 quad 2 < 4$

log 0.1 0.01 = 2

log 0.1 0.0001 = 4

$0.01 > 0.001 quad 2 < 4$

log 10 0.1 = - 1

log 10 0.01 = - 2

$0.1 > 0.01 quad -1 > -2$

Logarytm naturalny i dziesiętny

W praktyce najczęściej stosuje się logarytmy o podstawie 2, $e$ oraz 10, stąd zapis:

$log 10 a = log a$ - logarytm dziesiętny (alternatywnie Briggsa lub zwyczajny)
$log e a = ln a$ - logarytm naturalny (którego podstawa $e = lim_{ntoinfty}left( 1+frac{1}{n} right)^n = 2.71828...$ )
$log 2 a = lg a$

Uwaga!
Oznaczenia $log$ , $lg$ oraz $ln$ mogą mieć inne niż powyższe znaczenie w literaturze obcojęzycznej, programach komputerowych i językach programowania!