Matura z matematyki - ~Funkcja potęgowa i jej własności

Matura z matematyki - ~Funkcja potęgowa i jej własności

Funkcja wykładnicza i logarytmiczna

Trygonometria

Ciągi liczbowe

Planimetria

Funkcja potęgowa

DEFINICJA

Funkcja potęgowa jest to funkcja określona wzorem $f (x) = x p$ .

Dziedzina funkcji potęgowej:

Jeśli $p in mathbb{N}_+$ , to $D_f=mathbb{R}$
Jeśli $p in mathbb{Z}$ , to $D_f = R backslash {0}$
Jeśli :
- dla $p > 0$ , to $D_f=mathbb{R}_+cup{0}$
- dla $p < 0$ , to $D_f=mathbb{R}_+$

Wykres

O wykładniku równym zero

W tym przypadku wykres jest dość prosty - wykresem funkcji jest prosta. Jedynym faktem do zaznaczenia jest to, że $D=mathbb{R} backslash {0}$ . Dziedzina jest bez zera, ponieważ wartość wyrażenia $00$ jest nieokreślona.

O wykładniku dodatnim parzystym

Wszystkie te wykresy przecinają się w trzech punktach o współrzędnych (0;0), (-1;1), a także (1;1).

Własności:

$D_f = mathbb{R}$
$ZW_f = mathbb{R}_+ cup {0}$
Miejsce zerowe funkcji: $x 0 = 0$
Wartości dodatnie: $f(x)>0 iff x in mathbb{R} backslash {0}$
Wartości ujemne: $f(x)<0 iff x in varnothing$ , funkcja nie przyjmuje wartości ujemnych
Ekstrema:
Minimum: dla $x = 0$ $f (x) = 0$
Maksimum: nie przyjmuje wartości największej
Monotoniczność:
Rośnie dla $x in (0,+infty)$
Maleje dla $x in (-infty,0)$
Funkcja nie jest różnowartościowa
Funkcja jest parzysta
Funkcja nie jest nieparzysta

O wykładniku dodatnim nieparzystym

Łatwo zauważyć, że wykresy te przecinają się w trzech punktach o współrzędnych (0;0), (-1;-1), a także (1;1).

Własności:

$D_f = mathbb{R}$
$ZW_f = mathbb{R}$
Miejsce zerowe funkcji: $x 0 = 0$
Wartości dodatnie: $f(x)>0 iff x in mathbb{R}_+ backslash {0}$
Wartości ujemne: $f(x)<0 iff x in mathbb{R}_- backslash {0}$
Ekstrema:
Minimum: nie przyjmuje wartości najmniejszej
Maksimum: nie przyjmuje wartości największej
Monotoniczność:
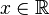
Rośnie dla $x in mathbb{R}$
Funkcja jest różnowartościowa
Funkcja nie jest parzysta
Funkcja jest nieparzysta

O wykładniku ujemnym parzystym

Wszystkie te wykresy przecinają się w dwóch punktach o współrzędnych (-1;1), a także (1;1). Ponadto zachodzi:

$y>1 iff x in (-1;0) cup (0;1)$

Własności:

$D_f = mathbb{R} backslash {0}$
$ZW_f = mathbb{R}_+$
Miejsce zerowe funkcji: brak
Wartości dodatnie: $f(x)>0 iff x in D_f$
Wartości ujemne: $f(x)<0 iff x in varnothing$
Ekstrema:
Minimum: nie przyjmuje wartości najmniejszej
Maksimum: nie przyjmuje wartości największej
Monotoniczność:
Rośnie dla $x in (-infty;0)$
Maleje dla $x in (0;+infty)$
Funkcja nie jest różnowartościowa
Funkcja jest parzysta
Funkcja nie jest nieparzysta
Asymptoty: $x = 0$ i $y = 0$

O wykładniku ujemnym nieparzystym

Wykresy te przecinają się w dwóch punktach o współrzędnych (-1;-1), a także (1;1). Można zauważyć, że zachodzi także:

$y>1 iff x in (0;1)$

Własności:

$D_f = mathbb{R} backslash {0}$
$ZW_f = mathbb{R} backslash {0}$
Miejsce zerowe funkcji: brak
Wartości dodatnie: $f(x)>0 iff x in D_f$
Wartości ujemne: $f(x)<0 iff x in varnothing$
Ekstrema:
Minimum: nie przyjmuje wartości najmniejszej
Maksimum: nie przyjmuje wartości największej
Monotoniczność:
Rośnie przedziałami $x in (-infty;0)$ i $x in (0;+infty)$
Funkcja jest różnowartościowa
Funkcja nie jest parzysta
Funkcja jest nieparzysta
Asymptoty: $x = 0$ i $y = 0$

Dzisiaj stronę odwiedzjużiło 18554 odwiedzający

Ta strona internetowa została utworzona bezpłatnie pod adresem Stronygratis.pl. Czy chcesz też mieć własną stronę internetową?

Darmowa rejestracja