Matura z matematyki - ~ Dziedzina funkcji

DEFINICJA

Dziedziną funkcji nazywamy zbiór wszystkich argumentów x, dla których funkcja ta jest określona.

Dziedzinę funkcji f najczęściej oznaczamy przez $D f$ .

Wyznaczanie dziedziny funkcji

Podczas wyznaczania dziedziny funkcji musimy pamiętać, że:

dzielenie przez zero jest niewykonalne, w przypadku ułamka mianownik musi być różny od 0,
liczba podpierwiastkowa nie może być ujemna
liczba podpierwiastkowa w mianowniku pewnego ułamka musi być liczbą dodatnią

Kiedy wyznaczamy dziedzinę pewnej funkcji, staramy się patrzeć prościej na to, co widzimy. Czyli kiedy zobaczymy taki prosty wzór:

$f(x) = frac{x^2}{x+2}$

Nasz tok rozumowania będzie wyglądał tak:

Jest to po prostu ułamek $frac{a}{b}$ , dlatego mianownik (czyli b) ma być różne od zera
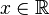
Zauważamy, że $a = x 2$ . Zastanawiamy się, czy jest tu jakiś ułamek lub pierwiastek, lecz na szczęście nie ma. Zatem w tym przypadku $x in mathbb{R}$
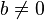Patrzymy na mianownik. Mamy $b = x + 2$ . Niestety, ponieważ jest to mianownik (pamiętamy „nigdy cholero nie dziel przez zero!”), musimy założyć, że $b neq 0$ , czyli $x+2 neq 0 implies x neq -2$ .
Na koniec podsumowujemy wszystko. Czyli odrzucamy wszystkie x, które zostały odrzucone w którymś punkcie. Czyli otrzymujemy $x neq -2$ , zatem dziedziną będzie $D_f = R backslash {-2}$ .

Spójrzmy teraz na bardziej skomplikowany

$f(x) = frac{sqrt{x-3}^2}{sqrt{x}(x-4)(x-3)}$

I znowu banał...

Mamy ułamek $frac{a}{b}$ , gdzie a może być dowolne, a b różne od zera
Patrzymy na licznik a. I znowu mamy a = c². Ponieważ kwadraty nas nie interesują, nie wpływają na dziedzinę funkcji patrzymy na c:
- No i mamy $c = sqrt{x-3}$ . Wiemy, że liczba podpierwiastkowa (w tym przypadku $x - 3$ ) musi być nieujemna, więc rozwiązujemy nierówność x $x - 3 geq 0$ i po prostym przekształceniu otrzymujemy $x geq 3$
Teraz patrzymy na mianownik , który ma być różny od 0. Wykorzystujemy własności mówiącą, że iloczyn pewnych liczb wynosi zero, gdy któraś z tych liczb jest równa 0. Czyli w skrócie . I rozwiązujemy, wykluczając te liczby:
- $d = 0 implies sqrt{x}=0 implies x=0$
- $e = 0 implies x-3 = 0 implies x=3$
- $f =0 implies x-4 = 0 implies x=4$
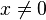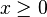Zatem $x neq 0$ , $x neq 3$ , $x neq 4$ . Ponadto, aby wyrażenie $sqrt{x}$ miało sens, x nie może być liczbą ujemną, zatem $x geq 0$ .
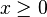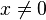I podsumowujemy: $x geq 3$ , $x geq 0$ , $x neq 0$ , $x neq 3$ , $x neq 4$ . Zatem $D_f = (3;+infty) backslash {4}$ .

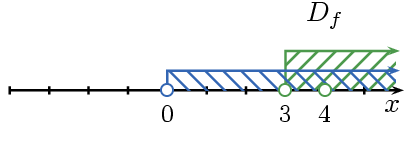
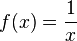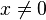Przykład 1. Określmy dziedzinę funkcji $f(x) = frac{1}{x}$ . Wyrażenie $frac{1}{x}$ ma sens liczbowy jedynie wtedy, gdy $x neq 0$ , ponieważ gdyby x było równe zeru musielibyśmy wykonać dzielenie przez 0, a wszyscy dobrze wiemy, że nie wolno dzielić przez 0 (1:0 nie ma sensu liczbowego). Wobec czego możemy wywnioskować, że $D_f=mathbb{R} backslash {0}$ .

Przykład 2. $f(x)=frac{3x+2}{(x-1)(x-2)}$ Aby określić dziedzinę musimy wyznaczyć te wartości x, dla których mianownik jest różny od zera, a następnie wykluczyć te liczby z dziedziny:

(x - 1)(x - 2) = 0

z własności iloczynu wiemy, że iloczyn ma wartość zero, jeśli którykolwiek z czynników ma wartości zero. Wobec czego:

x - 1 = 0 lub x - 2 = 0

x = 1 lub x = 2

Czyli $D_f=mathbb{R} backslash {1,2}$ .

Przykład 3. $f(x)=frac{2x+2}{sqrt{x-2}}$ Ponieważ liczba podpierwiastkowa musi być liczbą nieujemną, ponadto mianownik nie może być równy zeru, więc liczba podpierwiastkowa musi być większa od zera. Czyli $x-2>0 Rightarrow x>2$ , a wtedy $D_f=(2;+infty)$ .

Przykład 4. $f(x)=frac{1}{x^2+4}$ Mianownik musi być różny od zera, wobec czego $x^2+4 neq 0 Rightarrow x^2 neq -4$ . Ponieważ kwadrat dowolnej liczby rzeczywistej jest nieujemny (czyli zawsze $x^2 geq 0$ ), więc $x 2$ nigdy nie będzie równy liczbie -4. Otrzymujemy $D_f=mathbb{R}$ .