Matura z matematyki - ~Rozwiązywanie równań i nierówności wykładniczych

Rozwiązywanie równań wykładniczych

Przykładami równań wykładniczych mogą być:

$3^x=27$

$left(2frac{1}{5}right)^{x-2}=15$

$left(frac{1}{2}right)^{frac{1}{2}x}=2^{x+2}$

$2^{2x}-5 sdot 2^x-10=0$

Schemat rozwiązywania równań wygląda tak:

Ustalamy dziedzinę.
Sprowadzamy równanie, aby miało takie same podstawy lub sprowadzamy je do równania kwadratowego albo jeszcze do innego równania, tworząc przy tym odpowiednie założenia. Z równości podstaw wynika równość wykładników.
Rozwiązujemy równanie.
Sprawdzamy, czy rozwiązania przekształconych równań spełniają nasze założenie.
Podajemy odpowiedź.

Przykład 1

Chcemy rozwiązać równanie $left(frac{1}{4}right)^{frac{1}{2}x-1}=16^{x+3}$ , możemy to zrobić w ten sposób:

Ustalamy dziedzinę:
$left(frac{1}{4}right)^{frac{1}{2}x-1}=16^{x+3},~D=mathbb{R}$
Sprowadzamy do tej samej podstawy:
$begin{align} (4^{-1})^{frac{1}{2}x-1}&=(4^2)^{x+3}\ 4^{-frac{1}{2}x+1}&=4^{2x+6} end{align}$
Z równości potęg wynika równość wykładników:
$begin{align} -frac{1}{2}x+1&=2x+6\ -2frac{1}{2}x&=5quadBig/:(-2frac{1}{2})\ x&=-2,~in D end{align}$
Zatem rozwiązaniem równania jest -2.
Możemy sprawdzić rozwiązanie:
$L=left(frac{1}{4}right)^{frac{1}{2}x-1}=left(frac{1}{4}right)^{frac{1}{2}(-2)-1}= left(frac{1}{4}right)^{-2}=16$
$P=16^{x+3}=16^{-2+3}=16$
Zatem $L=P$

Przykład 2

Jeśli chcemy rozwiązać równanie $2^x+2^{7-x}=24 !$ , możemy to zrobić w ten sposób:

Ustalamy dziedzinę i przekształcamy równanie:
$2^x+2^{7-x}=24 ,~D=mathbb{R}$
$2^x+frac{2^7}{2^x}=24$
Podstawiamy $2^x=t, t in mathbb{R}_+$
$t+frac{128}{t}=24$ $/ sdot t$
$t^2-24t+128=0$
Otrzymujemy:
$t_1=8=2^3,~in mathbb{R}_+$
$t_2=16=2^4,~in mathbb{R}_+$
Ponieważ $2^x=t$ :
$2^x=t_1$ lub $2^x=t_2$
$2^x=2^3$ lub $2^x=2^4$
$x=3$ lub $x=4$
Liczby 3 i 4 są rozwiązaniami tego równania.

Rozwiązywanie nierówności wykładniczych

Przykładami nierówności wykładniczych są:

$2^x > left(frac{1}{2}right)^{2-xfrac{1}{2}}$

$3^{x^2-2}<3sqrt{3}$

$left(frac{1}{9}right)^x>3^{4-frac{1}{2}x}$

W celu rozwiązania nierówności wykładniczej należy:

Ustalić dziedzinę
Sprowadzić obie strony do tych samych podstaw albo przekształcić do innego równania, które potrafimy rozwiązać.
Wykorzystujemy własności funkcji wykładniczej, przekształcając odpowiednio równanie:
dla $a in (1;+infty)$
$a^n>a^m iff n>m$
$a^n<a^m iff n<m$
analogicznie dla porównań „mniejszy bądź równy”, czy też „większy bądź równy”

dla $a in (0;1)$
$a^n>a^m iff n<m$
$a^n<a^m iff n>m$
analogicznie dla porównań „mniejszy bądź równy”, czy też „większy bądź równy”
Rozwiązujemy otrzymane równanie.
Udzielamy odpowiedzi.

Popatrzmy jeszcze raz na punkt trzeci. Wynika z niego, że jeśli mamy równanie $2^{2x-1} geq 2^{3-x}$ , możemy je przekształcić na równanie $2x-1 > 3-x$ , ponieważ $a=2 in (1;+infty)$ . Natomiast $left(frac{1}{2}right)^{2x-1} > left(frac{1}{2}right)^{3-x} iff 2x-1 < 3-x$ , ponieważ $a=frac{1}{2} in (0;1)$ .

Przykład 1

Chcemy rozwiązać nierówność $left(frac{1}{4}right)^x>left(frac{1}{2}right)^frac{2x}{x+1}$ . W tym celu:

Ustalamy dziedzinę:
$left(frac{1}{4}right)^x>left(frac{1}{2}right)^frac{2x}{x+1},~D=mathbb{R} backslash {-1}$
Sprowadzamy do tych samych podstaw:
$left[left(frac{1}{2}right)^2right]^x>left(frac{1}{2}right)^frac{2x}{x+1}$
$left(frac{1}{2}right)^{2x}>left(frac{1}{2}right)^frac{2x}{x+1}$
Ponieważ 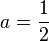$a=frac{1}{2}$ , wykorzystujemy prawo $a^n>a^m iff n<m$ :
$2x<frac{2x}{x+1}$
Przenosimy wszystko na jedną stronę i sprowadzamy do wspólnego mianownika:
$2x-frac{2x}{x+1}<0$
$frac{2x^2}{x+1}<0$
Z własności $frac{a}{b}<0 iff ab<0$ , wynika że:
$2x^2(x+1)<0 Rightarrow x_1=0$ , krotność 2 i $x_2=-1 !$ o krotności 1.
Czyli $x in (-infty;-1)$