Matura z matematyki - ~ Inne własności funkcji

Dla funkcji możemy określić zbiór tych argumentów, dla których funkcja jest dodatnia, a także zbiór tych argumentów, dla których funkcja jest ujemna.

Różnowartościowość funkcji

DEFINICJA

Funkcja $f: X rightarrow Y$ jest różnowartościowa wtedy i tylko wtedy, gdy funkcja ta różnym argumentom przyporządkowuje różne wartości.

$forall_{x_1, x_2 in X and x_1 neq x_2} f(x_1) neq f(x_2)$

Przykład 1. Funkcja $f (x) = x$ jest różnowartościowa, co łatwo zauważyć na wykresie. Żadne dwa punkty należące do wykresu, nie są na tej samej wysokości (nie mają takiej samej współrzędnej y).

Różnowartościowość tej funkcji wynika także z tego, że jest to funkcja rosnąca.

Przykład 2. Poniższa funkcja także jest różnowartościowa.

Zauważmy, że jeśli funkcja jest rosnąca lub malejąca, to jest także różnowartościowa.

Parzystość i nieparzystość funkcji

DEFINICJA

Funkcję f nazywamy parzystą wtedy i tylko wtedy, gdy dla każdej liczby x należącej do dziedziny funkcji, liczba przeciwna -x również należy do dziedziny tej funkcji oraz zachodzi $f (x) = f ( - x)$ .

$forall x in D_f: -x in D_f and f(x)=f(-x)$

Przykład 1. Funkcja $f (x) = x 2$ jest parzysta, ponieważ $f (x) = x 2 = ( - 1) 2 x 2 = ( - x) 2 = f ( - x)$ i $x in D_f mbox{ oraz } -x in D_f$ , zatem spełnia warunki określone w definicji.

Zobaczmy teraz na wykres:

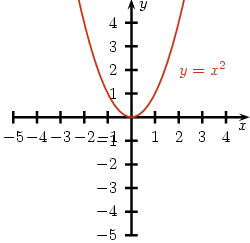
Zauważmy, że funkcja jest parzysta jeśli jest symetryczna względem osi OY.

Przykład 2. Funkcja $f (x) = | x |$ jest parzysta, ze względu na to, że zachodzi $f (x) = | x | = | - x | = f ( - x)$ . Poza tym widzimy symetrię na wykresie funkcji.

DEFINICJA

Funkcję f nazywamy nieparzystą wtedy i tylko wtedy, gdy dla każdej liczby x należącej do dziedziny funkcji, liczba przeciwna -x również należy do dziedziny tej funkcji oraz zachodzi równość $- f (x) = f ( - x)$ .

$forall x in D_f: -x in D_f and -f(x)=f(-x)$

Funkcja nieparzysta jest symetryczna względem punktu (0,0).

Przykład 3. Funkcja $f (x) = 3 x$ jest nieparzysta, ponieważ $- f (x) = - 3 x = 3( - x) = f ( - x)$

Przykład 4. Funkcja $f (x) = x 3$ jest nieparzysta.

Zachodzi $-f(x) = -x^3 = (-1)^3 cdot (-x)^3 = f(-x)$ .

Okresowość

DEFINICJA

Funkcję f nazywamy okresową wtedy i tylko wtedy, gdy istnieje taka liczba T różna od zera, że dla każdej liczby x należącej do dziedziny funkcji, liczby x+T oraz x-T również należą do dziedziny tej funkcji oraz zachodzi $f (x + T) = f (x)$ . Liczba T nazywana jest okresem tej funkcji.

$exist_{T neq 0} forall_{x in D_f} (x+T) in D_f and (x-T) in D_f and f(x+T)=f(x)$

Przykład 5.

Poniższa funkcja jest okresowa:

Okres tej funkcji wynosi 2, ponieważ $f (x) = f (x + 2)$ .

Przykład 6.

Funkcja $y = sin x$ jest funkcją okresową. Okres tej funkcji wynosi $2π$ .