Matura z matematyki - ~ Sposoby określania funkcji

Funkcję możemy przedstawić za pomocą:

opisu słownego
tabelki
wzoru
grafu
zbioru par uporządkowanych
wykresu

Przykład 1. Mamy daną funkcję określoną opisem słownym: „Dane są zbiory $X = { - 1,0,1,2,3}$ i $Y = {0,1,4,9}$ , wówczas każdej liczbie ze zbioru X przyporządkowujemy kwadrat tej liczby.”

funkcję tę możemy przedstawić w postaci tabelki:

x	-1	0	1	2	3
y	1	0	1	4	9

za pomocą wzoru:
$y=x^2 mbox{ dla } x in {-1,0,1,2,3}$
używa się także zapisu $f (x) = x 2$ , a także $f colon x mapsto x^2$
używając do tego grafu

zbioru par uporządkowanych:
${( - 1,1),(0,0),(1,1),(2,4),(3,9)}$
wykresu:

Przykład 2. Opiszmy funkcję 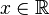$y = frac{2}{5}x-1$ , gdzie $x in mathbb{R}$ za pomocą różnych metod.

Opis słowny:
Każdej liczbie rzeczywistej x przyporządkowujemy różnicę iloczynu tej liczby z $frac{2}{5}$ i jedynki.
Za pomocą wzoru:
Wzór już mamy w przykładzie: $y = frac{2}{5}x-1$ .
Możemy także zapisać: $g(x) = frac{2}{5}x - 1$ , czy też $g colon x mapsto frac{2}{5}x - 1$ .
W postaci tabeli:
Ponieważ w tabelce nie możemy umieścić wszystkich liczb, możemy co najwyżej wybrać niektóre z nich. Tabelka może wyglądać tak:

x	-3	-2	-1	0	1	2	3
y	-2.2	-1.8	-1.4	-1	-0.6	-0.2	0.2

Rysując wykres funkcji

Używając zbioru par uporządkowanych:
Nie możemy wypisać wszystkich uporządkowanych par. Podobnie jak to było w przypadku tabelki wypiszemy tylko niektóre:
..., $( - 2, - 1.8)$ , ..., $( - 1, - 1.4)$ , ..., $(0, - 1)$ , ..., $(1, - 0.6)$ , ..., $(2, - 0.2)$ , ...
Raczej ciężko by było przedstawić tę funkcję w postaci grafu, musielibyśmy podobnie się „nakropkować”, jak w poprzednim przykładzie, dlatego ten sposób pominiemy.