Matura z matematyki - ~ Najmniejsza i największa wartość funkcji

DEFINICJA

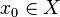Funkcja $f: X rightarrow Y$ przyjmuje wartość największą $y 0 = f (x 0)$ dla pewnego $x_0 in X$ wtedy i tylko wtedy, gdy dla każdego $x in X$ zachodzi nierówność $f(x) leq f(x_0)$ .

DEFINICJA
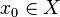Funkcja $f: X rightarrow Y$ przyjmuje wartość najmniejszą $y 0 = f (x 0)$ dla pewnego $x_0 in X$ wtedy i tylko wtedy, gdy dla każdego $x in X$ zachodzi nierówność $f(x) geq f(x_0)$

Przykład 1. Funkcja $y = x 2$ przyjmuje wartość najmniejszą $y 0 = 0$ (dla $x 0 = 0$ ).

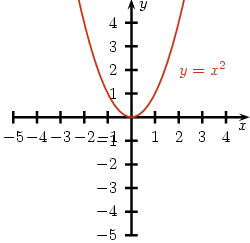
Funkcja ta nie przyjmuje wartości największej, jednak w pewnym przedziale np. $A = [1frac{1}{2};2]$ możemy taką znaleźć. W przedziale A będzie to $y m a x = 4$ dla $x = 2$ , natomiast najmniejszą wartością funkcji w tym przedziale będzie $y_{min} = left(1frac{1}{2}right)^2 = frac{9}{4}$ , dla $x = 1frac{1}{2}$ .

Przykład 2.

Największa wartości funkcji $y = 2-sqrt{2-2x}$ wynosi $y 0 = 2$ dla $x 0 = 1$

Wartością najmniejszą w przedziale $B = [ - 2;1)$ będzie $y_0 = f(-2) = 2 - sqrt{2-2cdot(-2)} = 2 - sqrt{6}$ . Nie możemy określić wartości największej w tym przedziale ze względu na to, że funkcja ta jest rosnąca w przedziale B i przedział jest lewostronnie otwarty. Możemy iść ciągle po wzdłuż tej funkcji, coraz wyżej i wyżej, lecz nigdy nie dojdziemy do 1.

Przykład 3.

Spójrzmy na poniższą funkcję, określoną dla $x in [-4;4]$ :

Przyjmuje ona zarówno wartość największa i najmniejszą. Funkcja ta przyjmuje wartość największą $y m a x = 3$ dla $x 1 = 2$ . Natomiast wartością najmniejszą tej funkcji jest $y m i n = - 3$ dla $x 2 = - 4$ .

Zwróćmy uwagę, że funkcja ta posiada pewne ala dwie „górki” i jedną „dolinę” położoną między nimi. Wszystkie te „górki” posiadają pewien „szczyt”, czyli miejsce, które jest położone najwyżej, natomiast „dolina” miejsce, które jest położone najniżej. Takie miejsca nazywane są ekstremami funkcji. Formalnie ekstremum funkcji definiuje się jako punkt, w którym funkcja zmienia swoją monotoniczność np. z rosnącej na malejącą.

Przykład 4.

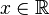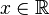Funkcja $y = 10$ posiada zarówno wartość najwyższą jak i najniższą. Wartością najniższą jest $y m i n = 10$ dla $x in mathbb{R}$ . Wartością najwyższą jest także $y m a x = 10$ i także dla $x in mathbb{R}$ .

W dowolnym niepustym przedziale (nawet otwartym), wartością najwyższa i najniższą będzie także 10.

Przykład 5.

Widzimy, że funkcja ta niestety nie przyjmuje wartości największej ani najmniejszej, ale na przykład możemy wziąć sobie przedział $A = [0;5]$ , wówczas wartością największą będzie 1 (dla $x = 5$ ), a najmniejszą -1 (dla $x = 0$ ).