Matura z matematyki - ~Rozwiązywanie równań i nierówności potęgowych

Rozwiązywanie równań potęgowych

Przykładami równań potęgowych może być:

$x^{frac{2}{3}}=9$ ,

$7x^{4}=2sqrt{7}$ ,

$x+x^{frac{1}{2}}=12$ .

W celu rozwiązania danego równania oczywiście najpierw należy wyznaczyć dziedzinę. Następnie rozwiązujemy je i sprawdzamy, które rozwiązania należą do dziedziny równania. Załóżmy, że mamy równanie $x^{frac{3}{2}}=sqrt{3}$ i chcemy je rozwiązać. Możemy to zrobić w ten sposób:

Ustalamy dziedzinę:
$x^{frac{3}{2}}= sqrt{3}, D=mathbb{R}_+ cup {0}$
Przekształcamy pierwiastek na potęgę:
$x^{frac{3}{2}}= 3^frac{1}{2}$
Ponieważ obydwie strony równania są dodatnie, możemy je podnieść do potęgi $frac{2}{3}$ :
$left(x^frac{3}{2}right)^frac{2}{3} = left(3^frac{1}{2}right)^frac{2}{3}$
Czyli:
$x=3^frac{1}{3}$

Niektóre równania możemy sprowadzić do postaci równania kwadratowego, na przykład równanie $x^frac{2}{5}+3x^frac{1}{5}=28$ :

Ustalamy dziedzinę:
$x^frac{2}{5}+3x^frac{1}{5}=28,~D=mathbb{R}_+ cup {0}$
Podstawmy: $x^frac{1}{5}=t,~t geq 0$ i otrzymujemy równanie kwadratowe:
$t 2 + 3 t - 28 = 0$
Czyli:
$t_1=-7,~notin D$
$t_2=4,~in D$
Otrzymujemy:
$x^frac{1}{5}=t_2=4$
$x = 4 5 = 1024$

Spójrzmy na jeszcze inny przykład: $sqrt{4x+5}-sqrt{2x-6}=3$ .

Ustalamy dziedzinę:
$4x+5 geq 0 and 2x-5 geq 0 iff x geq -frac{5}{4} and x geq frac{5}{2} iff x geq frac{5}{2}$
Czyli: $D=left[frac{5}{2};+inftyright)$
Wyrażenie to możemy podnieść do kwadratu, ponieważ lewa i prawa strona jest dodatnia:
$begin{align} (sqrt{4x+5}-sqrt{2x-6})^2&=9\ 4x+5-2sqrt{(4x+5)(2x-6)}+2x-6&=9\ -2sqrt{8x^2-14x-30}&=-6x+10quadBig/:(-2)\ sqrt{8x^2-14x-30}&=3x-5 end{align}$
Żeby równanie to miało sens muszą zachodzić warunki:
$x in left[frac{5}{2};+inftyright) and 8x^2-14x-30 geq 0 and 3x-5 geq 0$
$iff x in left[frac{5}{2};+inftyright) and x in left(-infty;-frac{4}{5}right] cup left[frac{1}{3};+infty;right) and x geq frac{5}{3}$
$iff x in left[frac{5}{2};+inftyright)$
I możemy ponownie podnieść to wyrażenie do kwadratu:
$8 x 2 - 14 x - 30 = (3 x - 5) 2$
$8 x 2 - 14 x - 30 = 9 x 2 - 30 x + 25$
$- x 2 + 16 x - 55 = 0$
Czyli:
$x_1=5,~in left[frac{5}{2};+inftyright)$
$x_1=11,~in left[frac{5}{2};+inftyright)$
Zatem rozwiązaniami tego równania jest 5 i 11.

Rozwiązywanie nierówności potęgowych

Przykładem nierówności potęgowej może być:

x 2 > x - 3

$x^frac{1}{2}-3x^frac{1}{4}+1>0$

$3x^frac{1}{6}>x^frac{1}{4}$

Aby rozwiązać nierówność potęgową możemy wykonać poniższe czynności:

Ustalamy dziedzinę.
Przenosimy wszystkie składniki nierówności na lewą stronę.
Rozwiązujemy nierówność, pamiętając o dziedzinie. Często okazuje się przydatne wykorzystanie własności:
1. $frac{a}{b}>0 iff ab>0$
2. $frac{a}{b}<0 iff ab<0$
Udzielamy odpowiedzi.

Czasami może okazać się pomocne obustronne pomnożenie nierówności przez $x k$ , gdzie k jest liczbą parzystą. Nie spowoduje to problemów, ponieważ $x k$ zawsze będzie nieujemne, a w związku z tym znak wyrażeń po obu stronach nierówności nie może ulec zmianie.

Przykład 1

Chcemy rozwiązać nierówność $x - 4 > x - 3$ .

Możemy to zrobić w standardowy sposób:

Ustalamy dziedzinę, wykonując pewne przekształcenia, które nam to ułatwią:
$x^{-4}>x^{-3},~D=mathbb{R} backslash {0}$
$frac{1}{x^4}>frac{1}{x^3}$
Przenosimy wszystko na lewą stronę:
$frac{1}{x^4}-frac{1}{x^3}>0$
Sprowadzamy do wspólnego mianownika:
$frac{1}{x^4}-frac{x}{x^4}>0$
$frac{1-x}{x^4}>0 iff x^4(1-x)>0$
$- x 4 (x - 1) > 0$
Otrzymujemy dwa miejsca zerowe:
$x 1 = 0$ o krotności 4
$x 2 = 1$ o krotności 1
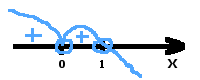
Rozwiązaniem nierówności jest $x in (-infty;0) cup (0;1)$

Nierówność $x - 4 > x - 3$ możemy także rozwiązać (po uprzednim ustaleniu dziedziny $D=mathbb{R} backslash {0}$ ) wymnażając obie strony przez $x 4$ , ponieważ $x 4 > 0$ dla każdego x różnego od 0. Otrzymalibyśmy wtedy:

$frac{1}{x^4}>frac{1}{x^3}$ $/ sdot x^4$

1 > x

Uwzględniając dziedzinę $D = mathbb{R} backslash {0}$ otrzymujemy, że $x in (-infty;0) cup (0;1)$ . Jak widać w tym przypadku drugi sposób okazał się o wiele łatwiejszy.

Trzeba dodać, że nie moglibyśmy wymnożyć przez np. $x 5$ (wykładnik nieparzysty), ponieważ $x 5$ może przyjąć wartość ujemną. A pamiętamy, że jeśli nierówność wymnażamy przez liczbę ujemną, musimy zmienić znak na przeciwny. Wymnażając przez $x 5$ nie jesteśmy w stanie stwierdzić, czy liczba ta jest ujemna, dodatnia, czy może jest zerem, zatem nie jesteśmy w stanie stwierdzić, czy musimy zmienić znak na przeciwny bez tworzenia dodatkowych założeń.

Dodajmy także, że jeśli wymnażamy obustronnie nierówność (czy nawet równanie) przez $x 4$ (czy inne potęgi) musimy sprawdzić jeden przypadek zdegenerowany -- co będzie gdy $x 4 = 0$ , czyli gdy $x = 0$ . Musimy to zrobić, ponieważ jeśli dowolną nierówność wymnożymy obustronnie przez 0 obie strony nierówności się zerują np. $x+5 geq 10$ przechodzi na $0 geq 0$ (zawsze prawdziwe). 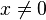Zatem musimy sprawdzić dwa przypadki -- czy liczba x = 0 spełnia niewymnożoną nierówność (w ten sposób pomijamy sytuację, gdy $x 4 = 0$ ), a także która z liczb $x neq 0$ spełnia wymnożoną nierówność (wtedy $x^4 neq 0$ ). Następnie sumujemy oba zbiory rozwiązań.

Na szczęście w powyższym przykładzie $D = mathbb{R} backslash {0}$ , czyli x nigdy nie będzie równy 0 i ten zdegenerowany przypadek nas nie dotyczy.