Matura z matematyki - ~Inne przykłady ciągów

Ciąg harmoniczny

Jeśli ciąg harmoniczny oznaczymy jako $(h n)$ , to k-ty wyraz będzie określony wzorem:

$h_k = frac{1}{k}$ .

Czyli na przykład $a_{10} = frac{1}{10}$ , $a_{13} = frac{1}{13}$ , a $a 1 = 1$ itp.

Nazwa pochodzi z fizyki, a dokładniej od tego, że w drgającej strunie kolejne możliwe do uzyskania długości fali stojącej są w stosunku $1:frac{1}{2}:frac{1}{3}:frac{1}{4}:dots$ .

Liczby harmoniczne

$H n$ , czyli n-ta liczba harmoniczna jest sumą kolejnych n wyrazów ciągu harmonicznego tzn.

$H_n = 1 + frac{1}{2} + frac{1}{3} + dots frac{1}{n}$ .

Zobaczmy kilka przykładów:

H 1 = 1

$H_3 = 1 + frac{1}{2} + frac{1}{3}$

$H_5 = 1 + frac{1}{2} + frac{1}{3} + frac{1}{4} + frac{1}{5}$

Oznaczenie $H n$ jako n-tą liczbę harmoniczną jest na powszechnie znane. Jeśli napiszemy $H n$ , to raczej wszyscy będą wiedzieli, że chodzi o n-tą liczbę harmoniczną.

Ciąg Fibonacciego

Ciąg ten zaczyna się od dwóch jedynek, a każdy następny wyraz jest sumą dwóch poprzednich. Ciąg ten oznaczamy przez $(F_n) = (1, 1, 2, 3, 5, 8, 13, 21, 34, dots)$ . Z definicji ciągu widzimy, że zachodzi relacja:

F 1 = 1

F 2 = 1

F n = F n - 1 + F n - 2 dla n > 2

Gdy $F 6 = 8$ i $F 7 = 13$ , wówczas $F 8 = F 7 + F 6 = 13 + 8 = 21$ . Podobnie, gdy wiemy, że:

F 44 = 701408733

F 45 = 1134903170

wtedy:

F 46 = F 45 + F 44 = 1134903170 + 701408733 = 1836311903

Ktoś kiedyś pokazał, że n-ty wyraz tego ciągu wynosi:

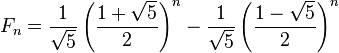$F_n = frac{1}{sqrt 5}left(frac{1 + sqrt 5}{2}right)^n - frac{1}{sqrt 5}left(frac{1 - sqrt 5}{2}right)^n$ (wzór Bineta)