W skrócie
- Wzory na miejsca zerowe
- dla Δ > 0 2 miejsca zerowe:
 ,
,
- dla Δ = 0 1 miejsce zerowe:
 ,
,
- dla Δ < 0 miejsca zerowe nie istnieją.
- Metoda wyciągania wspólnego czynnika
- równanie postaci np. x2 + x = 0
- przekształcamy do x(x + 1) = 0, po czym rozwiązujemy: x=0 oraz (x+1) = 0.
- Wzory skróconego mnożenia
- np.

- np.

- Równanie dwukwadratowe
- równanie postaci
 rozwiązujemy metodą podstawiania,
rozwiązujemy metodą podstawiania,
- przy założeniu t = x2 rozwiązujemy
 ,
,
- uzyskane pierwiastki
 , które spełniają założenie (tzn. musi być t>0) są pierwiastkami równania dwukwadratowego.
, które spełniają założenie (tzn. musi być t>0) są pierwiastkami równania dwukwadratowego.
Miejsca zerowe trójmianu kwadratowego
TWIERDZENIE
Dany jest trójmian kwadratowy ax2 + bx + c o współczynnikach rzeczywistych,  .
.
1. Jeżeli  , to trójmian ten ma 2 miejsca zerowe, które oblicza się ze wzorów:
, to trójmian ten ma 2 miejsca zerowe, które oblicza się ze wzorów:
2. Jeżeli  , to trójmian ma jedno miejsce zerowe, poprzednie wzory sprowadzają się do:
, to trójmian ma jedno miejsce zerowe, poprzednie wzory sprowadzają się do:
3. Jeżeli

, to trójmian kwadratowy nie ma miejsc zerowych w zbiorze liczb rzeczywistych.
Dowód (informacje dodatkowe)
Wyjdźmy z postaci kanonicznej trójmianu, którą już wcześniej udowodniliśmy i przyrównajmy ją do zera, aby znaleźć miejsca zerowe:



Przyjrzyjmy się teraz podanej postaci. Po lewej stronie mamy wyrażenie nieujemne (bo: dowolna liczba (w nawiasie) podniesiona do kwadratu da nam liczbę dodatnią). Po prawej stronie mianownik wyrażenia jest zawsze dodatni (4a2 > 0). Wszystko więc zależy od licznika. Rozpatrzmy wszystkie przypadki:
1. Gdy Δ < 0, to po prawej mamy wartość ujemną (iloraz dodatniej i ujemnej daje ujemną), a skoro po lewej mieliśmy wartość dodatnią - sprzeczność. Równość nie jest spełniona nigdy (w twierdzeniu: nie ma miejsc zerowych).
2. Gdy Δ = 0, wyrażenie po prawej stronie przyjmuje wartość zero, otrzymujemy:

/ Pierwiastkujemy obustronnie

Jest to nasze miejsce zerowe. Zwróć uwagę, że jest to współrzędna wierzchołka paraboli funkcji (dlaczego?).
3. Gdy
Δ > 0, otrzymujemy:

/ Pierwiastkujemy obustronnie i korzystamy z
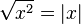

Rozwiązujemy równanie z wartością bezwzględną:
Przypadek 1: dla  - opuszczamy moduł bez zmiany znaku.
- opuszczamy moduł bez zmiany znaku.


Przypadek 2: dla  - opuszczamy moduł ze zmianą znaku:
- opuszczamy moduł ze zmianą znaku:


Tak więc, dla
Δ > 0 rozwiązaniami są

oraz

.
Przykłady - równania kwadratowe
Rozwiąż równania:
- Przykład 1. x2 − 3x − 4 = 0
- Przykład 2. x2 − 4 = 0
- Przykład 3. x2 − 6x + 9 = 0
- Przykład 4. x2 − 2x = 3x + 5
- Przykład 5. − x2 − 2x = 0
- Przykład 6. x2 − 5x + 22 = 0
- Przykład 7. x4 − 3x2 + 4 = 0 (równanie dwukwadratowe)
- Przykład 8. x2 + 6x − 7 = 0
- Przykład 9. x2 − 4 | x | − 12 = 0 (równanie z modułem)
Przykład 1
x2 − 3x − 4 = 0
Każde równanie kwadratowe można rozwiązać wykorzystując wyróżnik trójmianu kwadratowego. W powyższym przykładzie współczynniki a, b oraz c wynoszą:  .
.



Teraz, gdy już wyliczyliśmy deltę, korzystamy ze wzorów na pierwiastki trójmianu kwadratowego (miejsca zerowe).






Równanie ma więc dwa rozwiązania:  i
i  .
.
Przykład 2
x2 − 4 = 0
Powyższe równanie można również rozwiązać przy użyciu delty, gdzie a = 1,b = 0,c = − 4. Aby jednak pokazać inne metody liczenia pierwiastków trójmianu, skorzystamy ze wzoru skróconego mnożenia:

Korzystamy z niego i zamieniamy trójmian x2 − 4 = 0 na postać iloczynową:

Z tego miejsca już możemy zobaczyć pierwiastki (miejsca zerowe). Jeśli zamiast x podstawimy 2 lub -2, równanie się wyzeruje (sprawdź!). Więc rozwiązaniami są: 2 oraz -2.
Przykład 3
x2 − 6x + 9 = 0
Powyższe równanie rozwiążemy dwoma sposobami. Przez deltę oraz przez wzór skróconego mnożenia.
Pierwszy sposób - przez deltę:



Delta jest równa zeru, więc równanie ma jedno rozwiązanie:


Drugi sposób - przez wzór skróconego mnożenia:

Przyrównujemy w myślach x2 − 6x + 9 = 0 i  ...
...
(x − 3)2 = x2 − 2 * 1 * 3 + 32
Otrzymujemy:

Podobnie jak w poprzednim przykładzie, widzimy miejsca zerowe. Jeśli podstawimy za x cyfrę 3, równanie się wyzeruje. Rozwiązaniem jest więc 3.
Uwaga: rozwiązywanie metodą wzorów skróconego mnożenia ma przydatną zaletę - przyspiesza obliczanie miejsc zerowych, można je niemal znajdować 'w pamięci'. Niestety, nie wszystkie równania dają się rozwiązać tym sposobem (wówczas trzeba wrócić do rozwiązywania z użyciem delty).
Przykład 4
x2 − 2x = 3x + 5
Najpierw przenosimy wszystkie wyrazy na jedną stronę (aby mieć 0 po drugiej stronie) i je redukujemy:
x2 − 5x − 5 = 0






Rozwiązaniami tego równania są liczby 
Przykład 5
− x2 − 2x = 0
Powyższy przykład rozwiążemy poprzez wyciągnięcie wspólnego czynnika przed nawias:


Powyższe równanie zachodzi gdy:</br x = 0 lub − x − 2 = 0
Udało się nam więc wyznaczyć rozwiązania wyciągając x przed nawias i uzyskując 2 równania liniowe (których rozwiązania są rozwiązaniami naszego przykładu). Pierwiastkami są więc liczby 0 oraz -2. Uwaga: powyższy sposób rozumowania będzie niezbędny do rozkładania niektórych wielomianów na czynniki pierwsze. Taki sposób skraca także czas liczenia pierwiastków.
Przykład 6
x2 − 5x + 22 = 0
Policzmy deltę:
a = 1,b = − 5,c = 22


Wystarczy zauważyć, że  - równanie nie ma więc rozwiązań.
- równanie nie ma więc rozwiązań.
Przykład 7
x4 − 3x2 − 4 = 0
Powyższe równanie jest równaniem stopnia czwartego i jest nazywane równaniem dwukwadratowym. Można je rozwiązać poprzez wstawienie pomocniczej zmiennej t.

Po podstawieniu otrzymamy następujące wyrażenie:

Tym sposobem, możemy rozwiązać pomocnicze równanie kwadratowe, a jego pierwiastki (o ile będą spełniały przyjęte założenie) będą też pierwiastkami równania dwukwadratowego.
Dalej rozwiązujemy, wyznaczając pierwiastki  oraz
oraz  .
.



Wyliczyliśmy wartości zmiennych pomocniczych. Jednak mamy policzyć wartość x. Wróćmy więc do równania (a jednośnie naszego założenia):

Jeśli podstawimy obliczone wcześniej wartości, będziemy w stanie policzyć x.
Najpierw, dla t=-1

Otrzymaliśmy następna funkcję kwadratową, która musimy rozwiązać by obliczyć wartość x.

Powyższe równanie nie ma pierwiastków, ponieważ  Zauważmy, że samo równanie
Zauważmy, że samo równanie  jest sprzeczne - wartość podniesiona do kwadratu nigdy nie będzie liczbą ujemną.
jest sprzeczne - wartość podniesiona do kwadratu nigdy nie będzie liczbą ujemną.
Podstawmy więc drugą wartość t równą 4.


Korzystamy z wzorów skr. mnożenia i otrzymujemy 
Równanie ma dwa rozwiązania: x1 = 2 i x2 = − 2 (patrz na przykład nr.2).
Po obliczeniu pierwiastków x1 i x2 dochodzimy do wniosku, że całe równanie ma tylko dwa rozwiązania chociaż równanie stopnia czwartego może mieć tych rozwiązań 4. Bardzo ważną rzeczą jest to, że rozwiązania t ujemne nie spełniają równania. Dlatego też przy stawianiu założenia  można dodać warunek
można dodać warunek 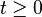 . Warunek ten sam wyjdzie podczas podstawiania wartości t (tak jak w przykładzie), jednak taki sposób jest wygodniejszy. Można więc powiedzieć, że równanie dwukwadratowe będzie miało 4 pierwiastki wtedy i tylko wtedy, gdy po podstawieniu zmiennej pomocniczej otrzymamy 2 pierwiastki dodatnie.
. Warunek ten sam wyjdzie podczas podstawiania wartości t (tak jak w przykładzie), jednak taki sposób jest wygodniejszy. Można więc powiedzieć, że równanie dwukwadratowe będzie miało 4 pierwiastki wtedy i tylko wtedy, gdy po podstawieniu zmiennej pomocniczej otrzymamy 2 pierwiastki dodatnie.
Przykład 8
x2 + 6x − 7 = 0
Ten przykład zrobimy dosyć nietypowym sposobem. Pomimo, że nie można tutaj zastosować bezpośrednio wzoru skróconego mnożenia to użyjemy go - w "sprytny" sposób.
x2 + 6x − 7 = 0 (*) - Podane wyrażenie oznaczamy jako (*) w celu uzyskania większej czytelności.
"Zwińmy" to wyrażenie za pomocą wzoru:
(x + 3)2 = 0 (**)
Powyższe wyrażenie nie jest równoważne wyrażeniu pierwotnemu (*). Po podniesieniu do potęgi otrzymamy bowiem: (x + 3)2 = x2 + 6x + 9. Uparcie chcemy jednak przejść z (*) do (**), aby jednak postawić znak równości, trzeba jedno z nich "wyrównać".
Skoro mamy otrzymać x2 + 6x − 7, to odejmijmy 16 od równania (**) - żeby "przywrócić równowagę": (x + 3)2 − 16
Popatrzmy na to teraz: Po podniesieniu do potęgi i odjęciu 16 otrzymamy x2 + 6x − 7 = 0. Jest to przecież nasze pierwsze równanie, (*). Czyli, można powiedzieć, że "zwinęliśmy", a następnie "wyrównaliśmy" to wyrażenie (zwróć uwagę, że jest to postać kanoniczna funkcji!).
Możemy więc zapisać: x2 + 6x − 7 = (x + 3)2 − 16.
Teraz po kolei liczymy:
(x + 3)2 − 16 = 0
(x + 3)2 = 16 / Pierwiastkujemy obustronnie


Korzystamy z własności: 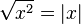 , po czym zostaje nam obliczyć równanie z wart. bezwzględną.
, po czym zostaje nam obliczyć równanie z wart. bezwzględną.
| x + 3 | = 4

W ten sposób policzyliśmy pierwiastki równania w nieco nietypowy sposób. Oczywiście, można przecież wszystko wyliczyć przez deltę, jednak taki sposób bardzo rozwija umiejętność rachowania. Pozwala także zrozumieć "naturę" funkcji kwadratowej oraz rozwija w nas umiejętność logicznego stosowania wzorów skróconego mnożenia. (umiejętności te mogą być przydatne przy rozwiązywaniu równań wielomianowych itd.)
Przykład 9

Żeby rozwiązać takie równanie, trzeba rozważyć dwa przypadki. Pierwszy, gdy 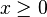 i drugi, gdy x < 0.
i drugi, gdy x < 0.
1 przypadek dla 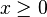
- Opuszczamy wartość bezwzględną bez zmiany znaku:
- x2 − 4x − 12 = 0
- Teraz rozwiązujemy tak, jak każde inne równanie. Ważne: na końcu porównujemy rozwiązania z założeniem
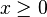 .
.



Wynikami pierwszego przypadku są liczby "-2" i "6". Jednak "-2" nie spełnia naszego początkowego założenia 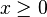 , więc nie jest rozwiązaniem.
, więc nie jest rozwiązaniem.
2 przypadek: dla 
- Opuszczamy wartość bezwzględną ze zmianą znaku w części pod modułem.
- x2 + 4x − 12 = 0



- Teraz x2 nie spełnia naszego założenia (x<0). Odrzucamy go więc.
Podsumowując, dochodzimy do wniosku, że równanie ma dwa rozwiązania: x1 = 6 i x2 = − 6.