Miara łukowa kąta
Narysujmy okrąg o promieniu r, a na nim zaznaczmy łuk L, dla którego kąt środkowy oparty o ten łuk będzie wynosił  . Znajdźmy wzór na długość tego łuku.
. Znajdźmy wzór na długość tego łuku.
Intuicyjnie długość łuku do obwodu okręgu jest równa mierze kąta w stopniach do  :
:

ponieważ Ob = 2πr, otrzymujemy:

zatem:

Jak łatwo zauważyć wartość  nie zależy od promienia naszego okręgu, tylko od kąta, który tworzy nasz łuk. Wartość ta nazywana jest miarą łukową kąta dla kąta
nie zależy od promienia naszego okręgu, tylko od kąta, który tworzy nasz łuk. Wartość ta nazywana jest miarą łukową kąta dla kąta  . W ogólności wzór na długość łuku wyznaczonego przez kąt
. W ogólności wzór na długość łuku wyznaczonego przez kąt  (wyznaczonego w stopniach) przybierze postać:
(wyznaczonego w stopniach) przybierze postać:

Tak jak długość nie musi wyrażać się w metrach, tak też kąt nie musi wyrażać się w stopniach. Możemy wykorzystać inną jednostkę kąta, jakim jest radian. Wtedy wartość kąta jest wyrażana w tzw. mierze łukowej. Załóżmy, że kąt  jest wyrażony w stopniach,
jest wyrażony w stopniach,  w radianach, wówczas wartości tych kątów wiąże zależność:
w radianach, wówczas wartości tych kątów wiąże zależność:

Jednostką miary łukowej jest radian, który w skrócie zapisywany jest przez rad. Często przy podawaniu kąta wyrażonego w mierze łukowej pomija się jednostkę np. zamiast  pisze się po prostu
pisze się po prostu  .
.
Powróćmy znowu do wzoru na długość łuku l, jednak tym razem jednak załóżmy, że kąt na którym jest oparty łuk jest wyrażony w radianach i wynosi α. Wówczas wykorzystując zależność  otrzymujemy zależność:
otrzymujemy zależność:

dzieląc obustronnie przez r otrzymujemy:

DEFINICJA
Miarą łukową kąta nazywamy stosunek długości łuku do długości promienia. Jest ona równa kątowi α, który wyznacza ten łuk:

Jednostką miary łukowej jest radian.
Ten drugi wzór jest o wiele łatwiejszy do zapamiętania.
Zauważmy, że miara kąta pełnego wyrażonego w stopniach wynosi  , a w radianach
, a w radianach  . Zatem:
. Zatem:
Aby zamienić stopnie na radiany możemy wykorzystać wcześniej wzór:
(który był przedstawiony wcześniej, lecz w nieco innej postaci).
Odwrotnie, aby zamienić radiany na stopnie wykorzystujemy wzór:
Możemy go o trzymać przekształcając poprzedni wzór.
Przykład 1 Zamieńmy miarę stopniową na miarę łukową
- a)

- b)

- c)

Wówczas możemy to zrobić na dwa sposoby:
- a) I sposób za pomocą proporcji:
- 2π -

- x -

- czyli:



- II sposób, wykorzystując wzór:


- b)

- c)

Przykład 2 Zamieńmy miarę łukową na miarę stopniową
- a)

- b)
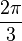
- b)

Podobnie jak w poprzednim przykładzie, możemy to zrobić na dwa sposoby:
- a) I sposób za pomocą proporcji:
- 2π -

 - x
- x
- zatem:




- II sposób, wykorzystując wzór:

- b)

- c)
