Matura z matematyki - ~ Działania arytmetyczne na liczbach rzeczywistych

Kolejność wykonywania działań:

Kolejność wykonywania działań jest nastepująca:

potęgowanie lub pierwiastkowanie,
mnożenie lub dzielenie (w zależności od kolejności),
dodawanie lub odejmowanie (kolejność także ważna).

Oczywiście jeśli gdziekolwiek występują nawiasy, to najpierw wykonujemy działania w nich zawarte. Przypomnijmy to sobie na kilku przykładach.

PRZYKŁAD 1.

$2 + 2 - 3 - 20:4 cdot 5$
Ze względu na nieobecność potęg przechodzimy od razu do mnożenie i dzielenia wykonując je w takiej kolejności, jakiej są zapisane – zaraz przed mnożeniem mamy dzielenie, więc wykonujemy je najpierw:
$2 + 2 - 3 - 20:4 cdot 5 = 2 + 2 - 3 - 5 cdot 5 = 2 + 2 - 3 - 25$ .
Teraz zostało tylko dodawanie i odejmowanie, więc dodajemy i odejmujemy zgodnie z kolejnością (od lewej do prawej):

2 + 2 - 3 - 25 = 4 - 3 - 25 = 1 - 25 = - 24

PRZYKŁAD 2.

$2^3 + 3^2 + sqrt{-1 + 5^2 - 16:4 cdot 6 : 3}$
Najpierw potęgowanie i pierwiastkowanie:
$2^3 + 3^2 + sqrt{-1 + 5^2 - 16:4 cdot 6 : 3} = 8 + 9 + sqrt{-1 + 25 - 16:4 cdot 6 : 3}$ .
Aby obliczyć pierwiastek musimy najpierw obliczyć wartość pod nim:

najpierw dzielenie i mnożenie pod pierwiastkiem (bo już nie ma pod nim potęg):

$8 + 9 + sqrt{-1 + 25 - 16:4 cdot 6 : 3} =$

$= 8 + 9 + sqrt{-1 + 25 - 4 cdot 6 : 3} =$

$= 8 + 9 + sqrt{-1 + 25 - 24 : 3} =$

$= 8 + 9 + sqrt{-1 + 25 - 8}$ ,

następnie dodawanie i odejmowanie pod pierwiastkiem:

$8 + 9 + sqrt{-1 + 25 - 8} = 8 + 9 + sqrt{24 - 8} = 8 + 9 + sqrt{16}$

i w końcu wyciągamy pierwiastek:

$8 + 9 + sqrt{16} = 8 + 9 + 4$ .

Następne na liście jest mnożenie i dzielenie, które nas nie dotyczy, pozostaje więc dodawanie i odejmowanie:

8 + 9 + 4 = 17 + 4 = 21

$PRZYKŁAD 3.$

2^{3+2} - sqrt{2^{3-2} : 2 cdot frac{9}{4}} = 2^5 -sqrt{ 2^1 : 2 cdot frac{9}{4}} = 32 - sqrt{frac{9}{4}} = 32 - frac{3}{2} = 30{,}5

$PRZYKŁAD 4.$

sqrt{(4^2 + 6^2):(2:13)} + 2 = sqrt{(16 + 36):frac{2}{13}} + 2 = sqrt{52 cdot frac{13}{2}} + 2= 13sqrt{2} + 2

$Wzory skróconego mnożenia$

(3+5)^2 = 3^2 + 2 cdot 3 cdot 5 + 5^2 = 9 + 30 + 25 = 64

(2 + 3) + 4 = 2 + (3 + 4)

, ponieważ

(2 + 3) + 4 = 5 + 4 = 9

, a także

2 + (3 + 4) = 2 + 7 = 9

Podobnie dla mnożenia:

$(3 cdot 5) cdot 2 = 3 cdot (5 cdot 2)$ , ponieważ

$(3 cdot 5) cdot 2 = 15 cdot 2 = 30$

i $3 cdot (5 cdot 2) = 3 cdot 10 = 30$ .

Prawo łączności nie sprawdza się w przypadku odejmowania i dzielenia. Zobaczymy to na dwóch przykładach:

$(8 - 5) - 2 = 3 - 2 = 1 neq 8 - (5 - 2) = 8 - 3 = 5$ , dosyć duża różnica.
$(12 : 2) : 3 = 6 : 3 = 2 neq 12 : (2 : 3) = 12 : frac{2}{3} = 12 cdot frac{3}{2} = 18$ , różnica jeszcze większa.

Innym prawem jest prawo redukcji (skreśleń):

jeśli $a + c = b + c$ , to $a = b$ (skreśliliśmy c),
jeśli $a sdot c=b sdot c$ i $c neq 0$ , to $a = b$ (także skreśliliśmy c)

Przykłady:

Jeśli $a + 10 = 20 + 10$ , to $a = 20$ .
Jeśli $a cdot 3 = 4 cdot 3$ , to $a = 4$ .

Kolejnymi prawami są prawa rozdzielności opisane niżej:

prawo rozdzielności mnożenia względem dodawania:
$a cdot (b+c)=a cdot b + a cdot c$
prawo rozdzielności mnożenia względem odejmowania:
$a cdot (b-c)=a cdot b - a cdot c$
prawo rozdzielności dzielenia względem dodawania:
$frac{(a+b)}{c}= frac{a}{c}+frac{b}{c}$
prawo rozdzielności dzielenia względem odejmowania:
$frac{(a-b)}{c}= frac{a}{c}-frac{b}{c}$

Zobaczmy na kilka przykładów:

$5 cdot (2 + 3) = 5 cdot 2 + 5 cdot 3 = 10 + 15 = 25$ ,

podobnie:

(25 - 10):5 = 25:5 - 10:5 = 5 - 2 = 3

a także:

$15 cdot 28 = 15 cdot (30-2) = 15 cdot 30 - 15 cdot 2 = 450 - 30 = 420$

Ważną obserwacją jest na przykład:

10 + 0 = 0 + 10 = 10

- 5 + 0 = - 5

$0 + 3frac{1}{2} = 3frac{1}{2}$

Ze względu na tę własność, mianowicie $a + 0 = 0 + a = a$ , liczba 0 jest nazywana elementem neutralnym dodawania. Niezależnie jaką liczbę byśmy dodali do 0, to i tak byśmy otrzymali tę samą liczbę.

Podobnie w przypadku mnożenia liczba 1 jest elementem neutralnym mnożenia, ponieważ $a cdot 1=1 sdot a=a$ np.

$10 cdot 1 = 10$ ,

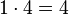$1 cdot 4 = 4$ ,

$-3 cdot 1 = -3$

Czy liczba 1 jest neutralna względem dzielenia? Nie. Co prawda zachodzi $a :1 = a$ , jednak $a : 1 neq 1 : a$ , np. $5 : 1 neq 1 : 5 = frac{1}{5}$ . Dla elementu neutralnego dane działanie musi być przemienne.

Nie wszystkie działania posiadają element neutralny, przykładami są wspomniane wyżej odejmowanie i dzielenie.

Dla każdej liczby rzeczywistej a istnieje dokładniej jedna liczba przeciwna (-a), która spełnia warunek:
$a + ( - a) = 0$ .
Na przykład liczbą przeciwną do 7 jest -7, do -1000 jest 1000, a do 0 jest też 0.
Dla każdej liczby rzeczywistej a różnej od 0 istnieje dokładnie jedna liczba odwrotna $mathbffrac{1}{a}$ spełniająca warunek:

$a sdot frac{1}{a}=1$ .
Liczbą odwrotną do 2 będzie $frac{1}{2}$ , do -10 będzie $-frac{1}{10}$ , do $frac{3}{7}$ będzie $frac{7}{3}$ , a do

- π

będzie $-frac{1}{pi}$ .

Na koniec przedstawimy ważną własność mnożenia, otóż iloczyn liczb rzeczywistych jest równy zero wtedy i tylko wtedy, gdy przynajmniej jeden z czynników jest równy 0:
$(a sdot b = 0)$ wtedy i tylko wtedy, gdy $a = 0 lub b = 0$ ,
np. $2 cdot a = 0$ jedynie wtedy, gdy $a = 0$ .