Matura z matematyki - ~ Równania i nierówności z parametrem

Równania i nierówności z parametrem

Przykład 1. Dla jakiej wartości parametru m równanie $x^2-m cdot x + 2=0$ ma dwa różnie miejsca zerowe?
Przykład 2. Dla jakiej wartości parametru m równanie $x^2-(m-2)cdot x+4=0$ ma jedno miejsce zerowe?
Przykład 3. Dla jakiej wartości parametru m równanie $(m^2-1)x^2+(m+1) cdot x+1 = 0$ ma jedno miejsce zerowe?
Przykład 4. Dla jakiej wartości parametru m nierówność $m cdot x^2 + (m+3) cdot x - m + 1 < 0$ jest spełniona w zbiorze liczb rzeczywistych?
Przykład 5. Dla jakiej wartości parametru m suma kwadratów pierwiastków równania $x^2 + (m-3) cdot x + m-2 = 0$ osiąga minimum?
Przykład 6. Dla jakiej wartości parametru m równanie $(1-m)x^2 - 2m cdot x + m + 2 = 0$ ma dwa różne rozwiązania ujemne?
Przykład 7. Dla jakiej wartości parametru m równanie $(1-m) cdot x^2 - 2m cdot x + m + 2 = 0$ ma dwa różne rozwiązania dodatnie?
Przykład 8. Ustal liczbę rozwiązań funkcji $left | x^2-6x+5 right | = m$ w zależności od parametru m, a następnie naszkicuj wykres funkcji h(x) obrazujący liczbę rozwiązań tego równania.
Przykład 9. Dla jakiej wartości parametru m równanie $x^2-4m cdot x+4m^2 - 1=0$ ma dwa różne rozwiązania należące do przedziału (-3,1)?

Przykład 1

Dla jakiej wartości parametru m równanie $x 2 - m x + 2 = 0$ ma dwa różne miejsca zerowe?

Wypiszmy współczynniki:

a = 1, b = -m, c = 2

Równanie ma dwa różne miejsca zerowe gdy $Δ > 0$ . Policzmy więc deltę:

$Delta = (-m)^2 - 4 cdot 1 cdot 2 = m^2 - 8$

Skoro równanie będzie miało dwa różne pierwiastki gdy $Δ > 0$ to musimy rozwiązać odpowiednią nierówność:

$m 2 - 8 > 0$

$(m-sqrt{8})cdot(m+sqrt{8}) > 0$ pomijamy szkicowanie wykresu, nierówność rozwiązujemy pamięciowo

$m_{1} = -sqrt{8}, m_{2} = sqrt{8}$

$m in (-infty, -sqrt{8}) cup ({sqrt{8}, +infty})$

Podany wynik warto sprawdzić podstawiając liczby należące i nienależące do przedziału.

W tym miejscu warto zwrócić uwagę na dokładnie ułożoną treść zadania - mamy policzyć kiedy równanie ma dwa różne miejsca zerowe. Gdy

Δ = 0

przyjmuje się, że funkcja ma dwa miejsca zerowe takie same . Gdybyśmy więc mieli obliczyć dla jakiej wartości parametru m funkcja ma dwa miejsca zerowe musielibyśmy postawić założenie $Delta ge 0$ , a nie

Δ > 0

. Jednak gdy mamy obliczyć kiedy funkcja ma dokładnie jedno miejsce zerowe to stawiamy założenie

Δ = 0

, co jest swoistym paradoksem. Należy więc zawsze dokładnie czytać treść zadania.

Przykład 2

Dla jakiej wartości parametru m równanie $x^2 - (m-2) cdot x + 4=0$ ma jedno miejsce zerowe?

Wypiszmy współczynniki:

a=1, b =-(m-2), c=4

Funkcja ma jedno miejsce zerowe gdy $Δ = 0$ . Obliczmy więc kiedy delta się zeruje.

$Delta = [-(m-2)]^2 - 4 cdot 1 cdot 4 = [-m+2]^2 - 4 cdot 1 cdot 4 = m^2 -4m + 4 - 16 = m^2 - 4m -12$

Teraz tworzymy drugą deltę i obliczamy miejsca zerowe równania $m 2 - 4 m - 12$

$Delta_{m} = (-4)^2 - 4 cdot 1 cdot (-12) = 16 + 48 = 64$

$sqrt{Delta_{m}} = 8$

$m_{1} = frac{4 - 8}{2} = -2$

$m_{2} = frac{4 + 8}{2} = 6$

Czyli funkcja ma jedno miejsce zerowe dla $m = - 2$ lub $m = 6$ . Podany wynik możesz z łatwością sprawdzić podstawiając w odpowiednie miejsca wartości m.

Przykład 3

Dla jakiej wartości parametru m równanie $(m^2-1) cdot x^2+(m+1) cdot x+1 = 0$ ma jedno miejsce zerowe?

Patrząc na ten przykład pozornie nie istnieje różnica pomiędzy nim, a przykładem poprzednim. Jest jednak jeden bardzo ważny element - co jeśli m będzie równe 1 lub -1? Wtedy po podstawieniu w odpowiednie miejsce współczynnik a "zwinie się", i otrzymamy funkcję liniową. Musimy więc rozpatrzeć tutaj 3 przypadki. Pierwszy gdy m=1, drugi gdy m=-1 i trzeci gdy $m neq 1$ i $m neq -1$ .

Bardzo ważne jest to, że nie wolno liczyć delty jeśli nie wiemy czy mamy do czynienia z funkcją liniową czy kwadratową - jest to wtedy błąd rzeczowy. Dlatego gdy parametr występuje przy wartości $x 2$ trzeba rozważyć kilka przypadków!

Pierwszy przypadek dla m= -1

$[(-1)^2-1) cdot x^2 + (-1+1) cdot x + 1 = 0$

$0 x 2 + 0 x + 1 = 0$

$1 = 0$

Otrzymaliśmy równanie sprzeczne. Więc parametr m=-1 nie spełnia równania.

Drugi przypadek dla m=1

$[1^2 -1] cdot x^2 + 2x + 1 = 0$

$0 x 2 + 2 x + 1 = 0$

$2 x = - 1$

$x = -frac{1}{2}$

Czyli funkcja ma jedno miejsce zerowe dla $m = 1$ .

Trzeci przypadek dla $m neq 1$ i $m neq -1$ . Teraz możemy policzyć deltę bez obawy, że rozwiązujemy równość liniową.

$Delta = (m+1)^2 - 4 cdot (m^2 -1) cdot 1 = m^2 + 2m + 1 - 4m^2 + 4 = -3m^2 + 2m + 5$

Znowu mamy równanie kwadratowe.

$Delta_{m} = 2^2 - 4 cdot (-3) cdot 5 = 4 + 60 = 64$

$sqrt{Delta_{m}} = 8$

$m_{1} = frac{-2 - 8}{-6} = frac{-10}{-6} = frac {5}{3}$

$m_{2} = frac{-2 + 8}{-6} = -1$

Jak widać -1 odpada na mocy założenia " $m neq 1$ i $m neq -1$ ". Gdybyśmy więc od razu obliczyli deltę to otrzymalibyśmy błędny wynik! Zawsze trzeba dokładnie przyjrzeć się przykładowi zanim zacznie się go rozwiązywać.

Równanie ma więc jedno miejsce zerowe dla $m = 1$ i $m=frac{5}{3}$ .

Przykład 4

Dla jakiej wartości parametru m nierówność $m cdot x^2 + (m+3) cdot x - m + 1 < 0$ jest spełniona w zbiorze liczb rzeczywistych?

Znowu mamy parametr przy $x 2$ . Zastanówmy się jak musi wyglądać wykres takiej nierówności aby była spełniona dla każdego x. Musi to być parabola całkowicie znajdująca się pod osią OX z ramionami skierowanymi w dół (pomijamy szkicowanie osi OY ponieważ nie ma ona żadnego wpływu na położenie naszej paraboli):

Może to być także stała (a = 0) funkcja liniowa, która znajduje się poniżej osi OX. Sprawdźmy więc co się dzieje gdy m=0.

1 przypadek m=0

$0 x 2 + 3 x - 0 + 1 < 0$

$3 x < - 1$

$x < -frac{1}{3}$

Nierówność jest spełniona tylko dla $x < -frac{1}{3}$ , czyli x nie należy do zbioru liczb rzeczywistych. Teraz zastanówmy się jak doprowadzić parabolę do stanu jak na ilustracji. Po pierwsze współczynnik kierunkowy a musi być mniejszy od 0. Po drugie, nie może być miejsc wspólnych z osią OX, czyli $Δ$ musi być mniejsza od 0. Otrzymamy w ten sposób układ dwóch warunków:

$begin{cases} a < 0 Delta < 0 end{cases}$

1. $a < 0 iff m < 0$

2. $Δ < 0$

$Delta = (m+3)^2 - 4 cdot m cdot (-m + 1)$

$m^2 + 6m + 9 - 4m cdot (-m + 1) < 0$

$m 2 + 6 m + 9 + 4 m 2 - 4 m < 0$

$5 m 2 + 2 m + 9 < 0$

$Delta_{m} = 2^2 - 4 cdot 5 cdot 9 = 4 - 180 = -176$

Delta jest zawsze dodatnia ( $a > 0$ i $Δ m < 0$ ). Czyli układ nigdy nie jest spełniony.

$m in varnothing$

Przykład 5

Dla jakiej wartości parametru m suma kwadratów pierwiastków równania $x^2 + (m-3) cdot x + m - 2 = 0$ osiąga minimum?

Zastanówmy się jakie warunki muszą zostać spełnione aby rozwiązać to zadanie:

$begin{cases} Delta ge 0 x_{1}^2+x_{2}^2 - min end{cases}$

Pierwszy warunek jest po to aby pierwiastki w ogóle istniały, drugi aby obliczyć minimum.

$Delta = (m-3)^2 - 4 cdot 1 cdot (m-2) = m^2 - 6m + 9 - 4m + 8 = m^2 - 10m + 17$

$Delta_{m} = (-10)^2 - 4 cdot 1 cdot 17 = 32$

$m_{1} = frac{10 - 4sqrt{2}}{2} = 5 - 2sqrt{2}$

$m_{1} = frac{10 + 4sqrt{2}}{2} = 5 + 2sqrt{2}$

$m in (-infty, 5 - 2sqrt{2}) cup ({5 + 2sqrt{2}, +infty})$

W poprzednim rozdziale wyprowadziliśmy wzór na sumę kwadratów pierwiastków, który wygląda następująco:

$(x_{1}+x_{2})^2 - 2x_{1}x_{2} = (frac{-b}{a})^2 - 2 cdot (frac{c}{a})$

Utwórzmy z tego funkcję i podstawmy odpowiednie wartości:

$f(m) = (frac{-m+3}{1})^2 - 2 cdot (frac{m-2}{1})$

$f(m) = m^2 - 6m + 9 - 2m + 4 = m^2 - 8m + 13$

Funkcja o współczynniku kierunkowym dodatnim osiąga minimum w punkcie wierzchołka:

$f_{min} = m_{w} = frac{8}{2} = 4$

Punkt $m=4 notin (-infty, 5 - 2sqrt{2}) cup ({5 + 2sqrt{2}, +infty})$ . Funkcja więc przyjmie najmniejszą wartość na jednym z krańców określoności:

$f(5 - 2sqrt{2}) = (5 - 2sqrt{2})^2 - 8 cdot (5 - 2sqrt{2}) + 13 = 25 - 20sqrt{2} + 8 - 40 + 16sqrt{2} = -7 -4sqrt{2}$

$f(5 + 2sqrt{2}) = (5 + 2sqrt{2})^2 - 8 cdot (5 + 2sqrt{2}) + 13 = 25 + 20sqrt{2} - 40 - 16sqrt{2} + 13 = -2 + 32sqrt{2}$

Funkcja osiąga minimum dla $m = 5 - 2sqrt{2}$

Przykład 6

Dla jakiej wartości parametru m równanie $(1 - m) x 2 - 2 m x + m + 2 = 0$ ma dwa różne rozwiązania ujemne?

Wskażmy warunki jakie muszą istnieć aby otrzymać poprawny wynik.

Od razu zauważamy, że współczynnik a musi być różny od 0. Ponieważ gdyby było równy zeru równanie kwadratowe "przeszło by" w równanie liniowe, które może mieć maksimum 1 rozwiązanie.

$a neq 0$

Teraz drugi warunek, aby istniały dwa różne pierwiastki:

$Δ > 0$

Aby istniały dwa pierwiastki ujemne ich iloczyn musi być dodatni, a suma ujemna. Dlaczego? Ponieważ iloczyn dowolnych liczb ujemnych jest dodatni (np. $-3 cdot -5 = 15$ ), a suma dowolnych liczb ujemnych jest ujemna (np. $- 3 + ( - 5) = - 8$ ). Mamy więc:

$x 1 + x 2 < 0$ i $x_{1} cdot x_{2} > 0$

Otrzymujemy w ten sposób układ, który należy rozwiązać:

$begin{cases} a neq 0 Delta > 0 x_{1} + x_{2} < 0 x_{1}cdot x_{2}>0 end{cases}$

1. $a neq 0 iff m neq 1$ - można odgadnąć pamięciowo.

2. $Delta = (-2m)^2 - 4 cdot (1-m) cdot (m+2) = 4m^2 - 4 (-m + 2 -m^2) = 4m^2 +4m -8 + 4m^2 = 8m^2 + 4m - 8 = 2m^2 +m - 2$

$Delta > 0 iff 2m^2 +m - 2 > 0$

$Delta_{m} = 1^2 - 4 cdot 2 cdot (-2) = 1+16 = 17$

$m_{1} = frac{-1 - sqrt{17}}{4}$

$m_{2} = frac{-1 + sqrt{17}}{4}$

$m in (-infty, -frac{1}{4} - frac{1}{4}sqrt{17}) cup (-frac{1}{4} + frac{1}{4}sqrt{17}, +infty)$

3. $frac{-b}{a} < 0$

$frac{2m}{1-m} < 0$

Podaną nierówność można rozwiązać poprzez zamianę ilorazu na iloczyn. Znak ilorazu jest taki sam jak znak iloczynu. Taka technika będzie jeszcze omawiana przy okazji funkcji homograficznej/wymiernej.

$frac{2m}{1-m} < 0 iff 2m(1-m) < 0$

$2 m (1 - m) < 0$

$m 1 = 0$

$m 2 = 1$

$m in (-infty, 0) cup (1, +infty)$

4. $frac{c}{a} > 0$

$frac{m+2}{1-m} > 0 iff (m+2)(1-m) > 0$

$m 1 = - 2$

$m 2 = 1$

$m in (-2, 1)$

Podane wyniki zaznaczamy na osi liczbowej (w przeciwnym wypadku łatwo się pogubić)

Wszystkie kolory przecinają się w przedziale:

$(-2, -frac{1}{4} - frac{1}{4}sqrt{17})$

który jest rozwiązaniem całego zadania.

$m in (-2, -frac{1}{4} - frac{1}{4}sqrt{17})$

Przykład 7

Tego przykładu już nie będziemy robić w całości. Wskażemy tylko prawidłowy tok myślenia.

Właściwie to spora część elementów jest taka sama jak w poprzednim przykładzie. Współczynnik a musi być różny od zera i delta większa od zera. Jednak aby istaniały dwa rozwiązania dodatnie muszą być jeszcze spełnione podane warunki:

$begin{cases} x_{1} cdot x_{2} > 0 x_{1} + x_{2} > 0end{cases}$

Iloczyn dwóch liczb dodatnich jest liczbą dodatnią, a ich suma także jest liczbą dodatnią. Mamy więc układ podobny jak w poprzednim przykładzie:

$begin{cases} a neq 0 Delta > 0 x_{1} cdot x_{2} > 0 x_{1} + x_{2} > 0end{cases}$

Przykład 8

Ustal liczbę rozwiązań funkcji $| x 2 - 6 x + 5 | = m$ w zależności od parametru m, a następnie naszkicuj wykres funkcji h(x) obrazujący liczbę rozwiązań tego równania.

Podany przykład najłatwiej rozwiązać metodą graficzną. Najpierw wprowadźmy pewne oznaczenia, które nam ułatwią rozwiązanie takiego zadania:

$begin{matrix} underbrace{ |x^2-6x+5| =} f(x) end{matrix} begin{matrix} underbrace{ m } g(x) end{matrix}$

Wyróżniliśmy w ten sposób dwie funkcję - jedna jest funkcją kwadratową z nałożoną wartościa bezwzględną, natomiast druga jest to funkcja o wzorze y=m (np. y=1, y=2, y=3 ... y=m, jest to funkcja liniowa, stała). W celu naszkicowania wykresu funkcji f(x) należy rozpatrzeć dwa przypadki - pierwszy, gdy wartość pod modułem jest mniejsza od 0, i drugi gdy jest większa bądź równa zeru. Skorzystamy jednak z pewnego ułatwienia, które już wcześniej miałeś okazję poznać w dziale Przekształcanie wykresu funkcji. Jako, że moduł jest nałożony na "całą" funkcję f(x) to przenosimy wszystko spod osi OX nad nią. Obliczmy najpierw wartości f(x).

$Δ = 16$

$x 1 = 1$

$x 2 = 5$

$p = 3$

$q = - 4$

Teraz nakładamy moduł i powstaje nam funkcja |f(x)|. Wygląda następująco (linią przerywaną jest oznaczona funkcja bez nałożenia modułu):

Wartość p nie zmienia się, jednak q zostaje symetrycznie odbite względem osi OX.

q' = 4

Teraz gdy już wiemy jak wygląda wykres funkcji f(x) zastanówmy się na funkcją g(x). Skoro jest to funkcja stała o dowolnej wartości to może ona przecinać funkcję f(x) w różnych miejscach:

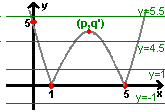
Punkty wspólne f(x) i g(x) to rozwiązania tych funkcji. Z łatwością odczytujemy więc z obrazka ilość rozwiązań:

0 rozwiązań dla $m in (-infty, 0)$

2 rozwiązańia dla $m = 0$

4 rozwiązania dla $m in (0, 4)$

3 rozwiązania dla $m = 4$

2 rozwiązania dla $m in (4, +infty)$

Ukończyliśmy w ten sposób pierwszą część zadania. Teraz pozotaje nam jeszcze szkic funkcji h(x). Jest to bardzo proste, i nie wymaga dłuższego tłumaczenia. Jest to po prostu obraz naszych wyników:

Przykład 9

Dla jakiej wartości parametru m równanie $x 2 - 4 m x + 4 m 2 - 1 = 0$ ma dwa różne rozwiązania należące do przedziału (-3,1)?

Zastanówmy się jakie założenia należy postawić aby ustawić w taki sposób pierwiastki. Już na początku zakładamy, że $Δ > 0$ aby istniały dwa różne rozwiązania. Dalej domyślamy się, że na pewno wierzchołek paraboli musi należeć do zbioru (-3,1) $((x_{w} in (-3,1))$ . Jednak sam ten warunek nie rozwiązuje całego problemu:

Pomimo, że wierzchołek znajduję się w podanym przedziale to pierwiastki nie należa do zbioru (-3,1). Na pierwszy rzut oka rozwiązanie całego problemu może się wydawać trudne, jednak jest ono bardzo proste. Wartość równania na krańcach przedziału musi być po prostu większa od zera:

Czyli inaczej $f ( - 3) > 0$ i $f (1) > 0$ .W ten sposób doprowadzamy parabolę do stanu, który jest podany w zadaniu. Mamy więc układ warunków:

$begin{cases} Delta > 0 x_{w} in (-3,1) f(-3) > 0 f(1) > 0 end{cases}$

1. $Δ > 0$

$Delta = (-4m)^2 - 4 cdot 1 cdot (4m^2-1) = 16m^2 - 16m^2 + 4 = 4$

$Δ = 4$ , czyli jest zawsze większa od 0. $Delta in R$

2. $x_{w} in (-3, 1)$

$frac{-b}{2a} in (-3, 1)$

$-3 < frac{-b}{2a} < 1$

$begin{cases} frac{-b}{2a} > -3 frac{-b}{2a}<1 end{cases}$

W tym miejscu nierówność podwójna, w celu uzyskania większej czytelności, została zapisana jako koniunkcja dwóch nierówności.

a) $frac{-b}{2a} > -3$