Matura z matematyki - ~ Działania na zbiorach

Suma zbiorów

Sumą zbiorów A i B nazywamy zbiór tych elementów, które należą do zbioru A lub do zbioru B, matematycznie zapisujemy ją tak: $A cup B = { x: x in A or x in B }$ .

Sumę zbiorów A i B ilustruje poniższy diagram Venna:

PRZYKŁAD:
Jeżeli $A = {1,2,5}$ i $B = {1,3,4}$ , to $A cup B={1,2,3,4,5}$ . Pomimo tego, że 1 występuje w obydwu zbiorach, w sumie tych zbiorów występuje tylko jeden raz.

Iloczyn zbiorów

Iloczynem zbioru A i B nazywamy zbiór tych elementów, które należą jednocześnie do zbioru A i do zbioru B, formalnie zapisujemy ją tak: 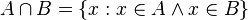$A cap B={ x: x in A and x in B }$ . Iloczyn zbiorów nazywany jest także częścią wspólną zbiorów lub przekrojem zbiorów.

Iloczyn zbiorów A i B ilustruje poniższy diagram Venna:

PRZYKŁAD:
Jeśli $A = {1,2,5}$ i $B = {1,3,4}$ , to 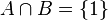$A cap B={1}$ . Liczba 1 jest jedynym wspólnym elementem tych zbiorów.

Różnica zbiorów

Różnicą zbiorów A i B nazywamy zbiór tych elementów, które należą do zbioru A, a które nie należą do zbioru B, możemy ją zapisać tak: $A backslash B = { x: x in A and x notin B }$ . Różnica zbiorów A i B zapisywana jest też $A - B$ .

Różnicę zbiorów A i B ilustruje poniższy diagram Venna:

PRZYKŁAD:
Jeśli $A = {1,2,5}$ i $B = {1,3,4}$ , to $A backslash B={2,5}$ . Jedynym wspólnym elementem obydwu zbiorów jest liczba 1, więc otrzymany zbiór będzie bardzo podobny do zbioru A, lecz nie posiadający liczby 1.

Dopełnienie zbioru

Dopełnieniem zbioru A z przestrzeni U nazywamy zbiór tych elementów przestrzeni U, które nie należą do zbioru A. Dopełnienie zbioru A oznaczamy jako $A'$ lub $A c$ . Dopełnienie możemy zapisać tak: $A'={ x: x in U and x notin A }$ .

Z definicji dopełniania wynika także, że jest to po prostu różnica przestrzeni U i zbioru A: $A'=U backslash A$ . Zbiór U zwany jest zbiorem uniwersum. Czasami zamiast U używa się innego oznaczenia przestrzeni np. X.

Dopełnienie zbiorów A i B ilustruje poniższy diagram Venna:

PRZYKŁAD 1:

Jeśli $A = {1,2,3}$ , a przestrzenią U jest zbiór wszystkich liczby całkowitych dodatnich, to dopełnieniem zbioru A będzie zbiór $A'={4,5,6,7,8,dots}$ .

PRZYKŁAD 2:

Jeśli $A = {2,3,5,6}$ , a przestrzenią U jest zbiór wszystkich liczby całkowitych dodatnich jednocyfrowych, to dopełnieniem zbioru A będzie zbiór $A' = {1,4,7,8,9}$ , ponieważ:

U = {1,2,3,4,5,6,7,8,9}

A = {2,3,5,6}

$A'=U backslash A={1,4,7,8,9}$

Podstawowe prawa rachunku zdań

$(A cup B)'=A' cap B'$ -- I prawo De Morgana
$(A cap B)'=A' cup B'$ -- II prawo De Morgana
$A cup B = B cup A$ -- przemienność dodawania zbiorów
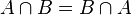
$A cap B = B cap A$ -- przemienność mnożenia zbiorów
$(A cup B) cup C = A cup (B cup C)$ -- łączność dodawania zbiorów
$(A cap B) cap C = A cap (B cap C)$ -- łączność mnożenia zbiorów
$A cup (B cap C) = (A cup B) cap (A cup C)$ -- rozdzielność dodawania zbiorów względem mnożenia
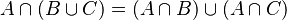
$A cap (B cup C) = (A cap B) cup (A cap C)$ -- rozdzielność mnożenia zbiorów względem dodawania

PRZYKŁAD:
Mamy zbiór

A = {1,2,3,4}

B = {1,3,5}

C = {3,5,9}

. Obliczyć $D=A cap (B cup C)$ :

$D=A cap (B cup C)=(A cap B) cup (A cap C)=$

$=({1,2,3,4} cap {1,3,5}) cup ({1,2,3,4} cap {3,5,9})=$

$={1,3} cup {3}={1,3}$