Matura z matematyki - ~Rozwiązywanie równań logarytmicznych

Rozwiązywanie równań logarytmicznych

DEFINICJA

Równaniem logarytmicznym nazywamy równanie, w którym niewiadoma występuje jedynie w wyrażeniu logarytmowanym lub w podstawie logarytmu. Przykładami równań logarytmicznych są:

$log 4 x = - 2$
$log x + 3 27 = - 2$
$log_{frac{1}{2}} 3-x = 1$

Wyznaczając rozwiązania równania logarytmicznego powinno się:

Ustalić dziedzinę
Rozwiązać równanie. Mogą się okazać przydatne poniższe własności logarytmów:
- $log_n b=x iff b=n^x$ np. $log_{frac{1}{2}} 3-x = 2 iff 3-x=left(frac{1}{2}right)^2$
- Z równości logarytmów o tych samych podstawach wynika równość liczb logarytmowanych np. $log_3 (x+3)=log_3 (x^2+1) iff x+3=x^2+1$ , ze względu na to, że funkcja logarytmiczna jest różnowartościowa.
Podać odpowiedź.

Przykład 1

Rozwiążmy równanie $log 2 x = 5$ .

Ustalamy dziedzinę: $x in mathbb{R}_+$
Własności $log_n b=x iff b=n^x$ sprawdzi się w tym przypadku. Otrzymamy
$log_2 x = 5 iff x = 2^5 = 32$
Odp. $x = 32$

Przykład 2

Chcemy rozwiązać równanie $log_3(4-frac{1}{5}x)=2$ . Możemy to zrobić w ten sposób:

Ustalamy dziedzinę:
$4-frac{1}{5}x>0 iff -frac{1}{5}x>-4 iff x<20$
Zatem mamy równanie $log_3(4-frac{1}{5}x)=2,~D=(-infty;20)$
Z własności $log_n b=x iff b=n^x$ i przekształcając odrobinę to równanie otrzymujemy:
$log_3(4-frac{1}{5}x)=2 iff 4-frac{1}{5}x=3^2$
$-frac{1}{5}x=5$
$x=-25,~in D$
Czyli rozwiązaniem tego równania jest -25.

Przykład 3

Rozwiążemy równanie $log 5 x 2 = 3$ .

Ustalamy dziedzinę:
Liczba logarytmowana musi być większa od 0, dlatego zakładamy, że $x^2 > 0 iff x neq 0$ . Zatem $D = mathbb{R} backslash {0}$ .
$log_5 {x^2} = 3 iff x^2 = 5^3 = 125$
I znajdujemy pierwiastki równania:
$x 2 - 125 = 0$
$(x - 5sqrt{5})(x + 5sqrt{5}) = 0$
czyli $x_1 = 5sqrt{5} in D$ i $x_2 = -5sqrt{5} in D$
Odp. $x in {-5sqrt{5}; 5sqrt{5}}$

Przykład 4

Rozwiążmy równanie $log^2_2 x - 10 log_2 x +16 = 0$ . (Pamiętamy, że $log^2_2 x = (log_2 x)^2$ , a nie $log 2 (x 2)$ .)

Ustalamy dziedzinę: $D = mathbb{R}_+$
Podstawiamy zmienną pomocniczą $t = log 2 x$ do równania $log^2_2 x - 10 log_2 x + 16$ i otrzymujemy:
$t 2 - 10 t + 16$
$Delta = 10^2 - 4 cdot 16 = 36$ , $sqrt{Delta} = 6$ .
$t_1 = frac{10-6}{2} = 2$ , $t_2 = frac{10+6}{2} = 8$
Ponieważ $t = log 2 x$ , więc:
$log 2 x = t 1 = 2$
$x = 2^2 = 4 in D$
lub $log 2 x = t 2 = 8$
$x = 2^8 = 256 in D$
Odp. $x in {4;256}$

Przykład 5

Spróbujmy rozwiązać równanie $log 2 x - log 4 x = 3$ .

Ustalamy dziedzinę: $D = mathbb{R}_+$
Obydwa logarytmy musimy sprowadzić do wspólnej podstawy. W tym celu wykorzystujemy wzór 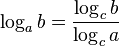$log_a b = frac{log_c b}{log_c a}$ . $log 4 x$ możemy zapisać jako $frac{log_2 x}{log_2 4} = frac{log_2 x}{2}$ . Zatem nasze równanie przybierze postać:
$log_2 x - frac{log_2 x}{2} = 3$
$frac{log_2 x}{2} = 3$
Obustronnie mnożymy przez 2:
$log 2 x = 6$
$x = 2 6 = 64$
Odp. $x = 64$

Przykład 6

Rozwiążmy równanie $2log_3 (x-3) - log_frac{1}{9} (x-3) = 5$

Ustalamy dziedzinę: $D = (3; +infty)$
Obydwa logarytmy podobnie jak w poprzednim przykładzie sprowadzamy do wspólnej podstawy otrzymując:
$2log_3 (x-3) - frac{log_3 (x-3)}{log_3 frac{1}{9}} = 5$
$2log_3 (x-3) - frac{log_3 (x-3)}{-2} = 5$
$frac{5}{2}log_3 (x-3) = 5$
Teraz obustronnie dzielimy przez $frac{5}{2}$ i mamy:
$log 3 (x - 3) = 2$
$x-3 = 3^2 = 9 implies x = 12$
Odp. $x = 12$

Przykład 7

Rozwiążmy równanie $2log x - 3 3 = 2$ .

Ustalamy dziedzinę pamiętając, że podstawa logarytmu musi należeć do sumy przedziałów $(0;1) cup (1;+infty)$ :
$x-3 in (0;1) cup (1;+infty)$
czyli $D = (3;4) cup (4;+infty)$
Skorzystamy z własności $k log a x = log a x k$ :
$2log_{x-3} 3 = 2 iff log_{x-3} 3^2 = 2$
zatem $log x - 3 9 = 2$
Ostatecznie otrzymujemy równanie kwadratowe:
$9 = (x - 3) 2$
$9 = x 2 - 6 x + 9$
$x (x - 6) = 0$
Otrzymujemy: $x_1 = 0 notin D$ i $x_2 = 6 in D$
Odp. $x = 6$