Matura z matematyki - ~ Oś liczbowa i układ współrzędnych na płaszczyźnie

Oś liczbowa

DEFINICJA

Oś liczbowa jest to prosta, na której wyróżniono kierunek, punkt zerowy oraz jednostkę.

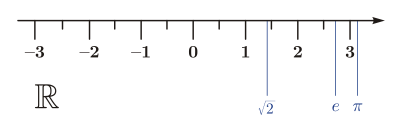
Możemy przyporządkować każdej liczbie rzeczywistej dokładnie jeden punkt na osi liczbowej czyli np. 1, -1000, $pi=3.1415dots$ . Taką liczbę nazywamy współrzędną. Na powyższym rysunku zostały wyróżnione punkty o współrzędnych całkowitych, a także położenie trzech często spotykanych liczb niewymiernych.

Układ współrzędnych kartezjańskich

Układ współrzędnych kartezjańskich (prostokątny) – prostoliniowy układ współrzędnych o prostopadłych do siebie osiach.

Układem współrzędnych kartezjańskich nazywamy układ współrzędnych w którym zadane są:

punkt zwany środkiem lub początkiem układu współrzędnych, którego wszystkie współrzędne są równe zeru, często oznaczany literą $O$ lub cyfrą $0$ .
zestaw n osi liczbowych zwanych osiami układu współrzędnych, z których każde dwie są do siebie prostopadłe i których zera znajdują się w wybranym początku układu. Dwie pierwsze osie często oznaczane są jako:
- $O X$ (pierwsza oś, zwana osią odciętych),
- $O Y$ (druga, zwana osią rzędnych),

Liczba osi układu współrzędnych wyznacza tzw. wymiar przestrzeni.

WSPÓŁRZĘDNE

Aby wyznaczyć k-tą współrzędną zadanego punktu $P$ :

Tworzymy rzut prostokątny punktu $P$ na k-tą oś, tzn. konstruujemy prostą przechodzącą przez $P$ i prostopadłą do k-tej osi a następnie znajdujemy punkt przecięcia tej prostej z k-tą osią.
Wartość w uzyskanym punkcie osi jest k-tą współrzędną $P$ .

Trzy pierwsze współrzędne są często oznaczane jako:

$x$ – odcięta, łac. abscissa,
$y$ – rzędna, łac. ordinata,
$z$ – łac. aplicata.

Właśnie ze sposobu wyznaczania współrzędnych punktu (poprzez rzut prostokątny) kartezjański układ współrzędnych zyskał również nazwę prostokątnego układu współrzędnych używanego przede wszystkim w szkołach.