Matura z matematyki - ~ Równania wielomianowe

Funkcja wykładnicza i logarytmiczna

Trygonometria

Ciągi liczbowe

Planimetria

Równania wielomianowe

Na początek definicja.

DEFINICJA

Równanie wielomianowe to równanie otrzymane poprzez przyrównanie danego wielomianu do zera.

Zobaczmy na przykłady:

$4 x + 1 = 0$
$3 x 2 + 2 x - 5 = 0$
$x 7 + x 6 + x 5 + x 4 + x 3 + x 2 + x 1 - 1 = 0$

Rozwiązywanie równania wielomianowego polega na znalezieniu wszystkich 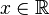$x in mathbb{R}$ , dla których wielomian jest równy zero. Niestety problem ten z reguły nie jest łatwy, jednak w standardowych zadaniach trzeba będzie z reguły skorzystać:

ze wzorów skróconego mnożenia
z dzielenie wielomianów i twierdzenie Bézout
z twierdzenia o pierwiastkach wymiernych
metody podstawiania (tzn. sprawdzamy, czy dla danego x zachodzi W(x) = 0)

Dzisiaj stronę odwiedzjużiło 18575 odwiedzający

Ta strona internetowa została utworzona bezpłatnie pod adresem Stronygratis.pl. Czy chcesz też mieć własną stronę internetową?

Darmowa rejestracja