Matura z matematyki - ~ Definicja wielomianu

Jednomian

Zacznijmy od czegoś prostego, czyli od zdefiniowania czym są jednomiany.

DEFINICJA

Jednomian to iloczyn czynników, w którym każdy czynnik jest liczbą lub pewną zmienną.

Jednomianem może być:

$4$
$x$
$2 a$
$3 a b c$
$4 b 3$
$123 a 2$

Wielomiany

Już znamy pojęcie jednomianu. Teraz kilka jednomianów możemy do siebie dodać np. do jednomianu $x$ możemy dodać $2 a$ otrzymując $x + 2 a$ . Innym przykładem sumy jednomianów może być:

$x 3 + y 2 + z 3$ ,
$frac{4}{3}x^7 + x^5 + x$ ,
$a 2 + 2 a b + b 2$ ,

a takie coś nazywamy wielomianami.

DEFINICJA

Wielomian to suma jednomianów.

Wielomiany możemy podzielić ze względu na liczbę zmiennych np. $- a 2 + b 2 + 4 c + d$ będzie wielomianem czterech zmiennych a, b, c i d. Wielomian $3 x + 2 y$ będzie wielomianem dwóch zmiennych x i y, a wielomian $4 x 2 + 3 x + 1$ będzie wielomianem jednej zmiennej x. W tym podręczniku mówiąc o wielomianach, będziemy mieli najczęściej na myśli właśnie wielomiany jednej zmiennej.

Wielomiany jednej zmiennej

Zauważmy, że wielomiany jednej zmiennej są pewną funkcją, dlatego też dany wielomian będziemy najczęściej zapisywać jako $W (x)$ , $P (x)$ , $Q (x)$ np.:

$W (x) = x 2 + 2 x - 1$ ,
$P (x) = 2 x - 1$ ,
$Q(x) = 2x^{123} - 2x^{122} + 2x^{121} - dots + 2x^3 - 2x^2 + 2x^1 - 2$ .

Przyjmujemy, że dziedziną wielomianu jednej zmiennej jest zbiór liczb rzeczywistych.

Zobaczmy teraz na poniższą, pełną definicję wielomianu jednej zmiennej.

DEFINICJA

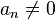Funkcja W określona wzorem $W(x)=a_nx^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+dots+a_1x^1+a_0$ , gdzie $a_n neq 0$ nazywana jest wielomianem jednej zmiennej stopnia n.

Liczby $a 0$ , $a 1$ , $a 2$ , ..., $a n$ nazywane są współczynnikami wielomianu. W wielomianie $W (x) = 6 x 3 + 4 x 2 + 3 x + 2$ współczynnikami będą $a 3 = 6$ , $a 2 = 4$ , $a 1 = 3$ i $a 0 = 2$ .

A ile wynosi współczynnik przy 23 potędze w wielomianie $2 x 3 + x$ ? Odpowiedź wydaje się prosta, $a 23 = 0$ , ponieważ $2 x 3 + x = 0 x 23 + 2 x 3 + x$ .

W powyższej definicji został wprowadzony stopień wielomianu. Stopień wielomianu to największe takie n, że 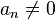$a_n neq 0$ np. $P (x) = 3 x 6 + x 2 + 1$ jest wielomianem 6. stopnia, ale wielomian $Q (x) = 0 x 100 + 23 x + 1$ jest wielomianem pierwszego stopnia, ponieważ $a 1 = 23$ i $a 100 = 0$ .

Zauważmy, że funkcja stała $f (x) = a$ jest wielomianem zerowego stopnia. Funkcja liniowa $f(x) = ax + b, a neq 0$ jest wielomianem pierwszego stopnia, a funkcja kwadratowa $g(x) = ax^2 + bx + c, a neq 0$ jest wielomianem drugiego stopnia.

Uporządkowanie wielomianu

Wielomiany mogą być uporządkowane rosnąco lub malejąco, według rosnących lub malejących wykładników potęg.

Wielomianami uporządkowanymi malejąco będą:

$W 1 (x) = 10 x 3 + 5 x 2 + 7 x + 10$ ,
$W 2 (x) = x 50 + 2 x 21 + 4 x$ ,
$W 3 (x) = x + 1$ .

Natomiast wielomianami uporządkowanymi rosnąco będą:

$P 1 (x) = 10 + 7 x + 5 x 2 + 10 x 3$
$P 2 (x) = 4 x + 2 x 21 + x 50$
$P 3 (x) = 1 + x$

Równość wielomianu

Wielomiany są funkcją, gdzie zbiorem wartości tej funkcji jest zbiór liczb rzeczywistych, zatem dwa wielomiany P i Q będą sobie równe, jeśli dla wszystkich $x$ zachodzi $P (x) = Q (x)$ , a z tego z kolei wynika poniższe twierdzenie, które przedstawimy bez dowodu:

TWIERDZENIE

Dwa wielomiany są równe wtedy i tylko wtedy, gdy współczynniki przy odpowiednich potęgach są sobie równe.

Na przykład wielomiany $A (x) = 10 x 3 + 3 x 2 + 4 x$ oraz $B (x) = 10 x 3 + 3 x 2 + 4 x$ są równe, ale $C (x) = 9 x 5 + 4 x 2 + x$ oraz $D (x) = 10 x 5 + 4 x 2 + x$ nie są równe. Podobnie wielomiany $W (x) = x 4 + x$ jest równy wielomianowi $P(x) = frac{2x + 2x^4}{2}$ , ale nie jest równy $P (x) = 2 x 4 + 2 x$ .

Wielomiany możemy do siebie dodawać i odejmować. W następnym podrozdziale dowiemy się, jak to robić.